okrąg fiki123: Jak rozwiązać to: https://sway.office.com/s/vF1ixy7zPBry1T9n/images/tRN6uVnTTlv3ZR?quality=816&allowAnimation=true kąt BAC=30^o, u góry przy A te kąty z dwoma łukami są równe.

ford: https://www.fotosik.pl/zdjecie/fe89444c7f9f247c |AS| = x P_BAS + P_SAC = P_BAC

1		1		1
	*6*x*sin15o +		*4*x*sin15o =		*6*4*sin30o
2		2		2

wyliczasz x Z własności czworokąta wpisanego w okrąg: jeśli kąt BAC = 30^o, to kąt BDC = 150^o Kąty wpisane BAD i DAC są równe, więc oparte są na równej długości łukach BD i DC Zatem |BD| = |DC| Trójkąt BDC jest równoramienny

	1800 − 1500
Kąt CBD = kąt BCD =		= 15o
	2

Z tw. cosinusów w ΔABS i ΔSAC |BS|² = 6² + x² − 2*6*x*cos15^o |CS|² = 4² + x² − 2*4*x*cos15^o Oznaczamy |BS| = a, |CS| = b Z tw. cosinusów w ΔSBD i ΔSDC masz układ równań z niewiadomymi |CD| = |BD| = c oraz |SD| = y {y² = a² + c² − 2a*c*cos15^o {y² = b² + c² − 2b*c*cos15^o z niego wyliczasz y Na koniec wyliczasz szukane |AD| = x + y

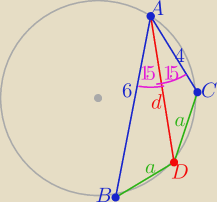Eta: |BD|=|DC| =a z tw. kosinusów a²=36+d²−12dcos15^o i a²= 16+d²−8dcos15^o

	5
to 4dcos15o=20 ⇒ d=
	cos15o

cos15^o= cos(45^o−30^o)=............

	√2
cos15o=		(√3−1)
	4

zatem d= ..........