Dla chętnych maturzystów
Saizou :
Jeśli ktoś z
maturzystów jest chętny, to zapraszam

Zad. 1
Przekątne trapezu ABCD przecinają się w punkcie M.
Wysokość trapezu ma długość 18.
Pole trójkąta ABM jest równe 25, pole trójkąta CDM jest równe 16.
Oblicz pole trapezu.
19 kwi 20:27
wredulus_pospolitus:
A myślałem że Saizou na solówkę zaprasza maturzystów

19 kwi 20:30
Saizou : Jestem smutny, bo nie działa mi logowanie

. Jakiś skrypt mnie nie przepuszcza na Safari.
(śmieszne bo tylko na MacBooku, a na Ipadzie normalnie idzie).
I robię za
czarną oFcę 
19 kwi 20:33
anonim123: Czy to można policzyć z podobieństw pól trójkątów?
19 kwi 20:38
Saizou : można

19 kwi 20:40
f123: 81
19 kwi 20:46
Saizou :
 fil
fil
19 kwi 20:46
Saizou :
To jeszcze obliczenia
 Zadanie 2
Zadanie 2
Wysokość H prawidłowego ostrosłupa sześciokątnego jest dwa razy większa
niż długość a krawędzie jego podstawy.
Oblicz cosinus kąta zawartego między sąsiednimi ścianami bocznymi tego ostrosłupa.
19 kwi 20:49
Shizzer: Ja to zrobiłem z podobieństw pól trójkątów, a mając podobieństwo pól miałem też
podobieństwo wysokości tychże trójkątów. Z tego już łatwo obliczyć długości podstaw trapezu
mając podane pola trójkątów i wysokość trapezu.
Da się jakoś inaczej do tego podejść?

19 kwi 20:53
Saizou :
Shizzer taka metoda jest najprostsza

19 kwi 20:57
salamandra: Ptrapezu=(√PABM+√PCDM)2=(√25+√16)2=81
19 kwi 20:57
Saizou :
salamandara nauka
Ety nie poszła w las

19 kwi 20:58
19 kwi 21:10
f123:
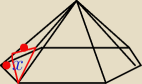
Zad 2
Pole jednego trojkata:
| | a√3 | |
htrojkata2 = ( |
| )2 + (2a)2 |
| | 2 | |
| | 1 | | a2√19 | |
P = |
| * a * htrojkata = |
| |
| | 2 | | 4 | |
Dlugosc krawedzi ostroslupa:
d
2 = a
2 + (2a)
2
d = a
√5
Obliczam 'x':
Tw cosinusow dla trojkata zaznaczonego kolorem czerwonym:
| | a√95 | | a√95 | | a√95 | |
(a√3) 2 = ( |
| )2 + ( |
| )2 − 2 * ( |
| )2 * cosα |
| | 10 | | 10 | | 10 | |
19 kwi 21:20
f123:
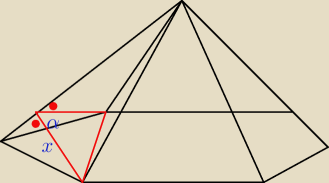
19 kwi 21:24
Saizou : Tak lepiej z tym rysunkiem

19 kwi 21:26
Saizou :
Zadanie 3
Sprawdź tożsamość:
19 kwi 21:29
19 kwi 21:41
Saizou : + założenia
Salamandra  Zadanie 4
Zadanie 4
Dany jest ciąg o wyrazie ogólnym a
n=
√n2+2n−
√n2−2n.
Wykaż, że a
n > 2 dla dowolnej liczby naturalnej n>1.
19 kwi 21:44
Szkolniak:
| | sin2x*cosx | | 2cos2x*sinx | |
L= |
| = |
| = |
| | (1+cos2a)(1+cosa) | | cosx+2cos2x+cos2x*cosx | |
| | 2cosx*sinx | | sinx | |
= |
| = |
| =P, cnw. |
| | 1+2cosx+cos2x | | 1+cosx | |
19 kwi 21:45
Saizou :
Szkolniak ładnie, sztuczka żeby wyeliminować kąty ułamkowe zawsze pomaga

19 kwi 21:46
19 kwi 21:47
Szkolniak: ad zad4:
Podnosimy po prostu do kwadratu i wychodzi, ze 2n2+1>0?
19 kwi 21:53
Saizou :
Szkolniak nie, jak podniosłeś do kwadratu?
19 kwi 21:56
Szkolniak: Czyli jednak nie mogę tak zrobić..
A gdybym zbadał funkcję f(x)=√x2+2x−√x2−2x?
Granica w +∞, rozwiązanie równania f(x)=2 (sprzeczne: 2x2+1=0), wartość funkcji w punkcie x=2?
Taki dowód by oddawał to co mamy wykazać w 100%?
19 kwi 22:05
f123: √n2 + 2n − √n2 − 2n > 2 |2
n2 + 2n − 2√n4 − 4n2 + n2 − 2n > 4
2(n2 − 2) > 2n√n2 − 4 |2
n4 − 4n2 + 4 > n4 − 4n2
4 > 0
c.n.u
19 kwi 22:14
Saizou :
Możesz podnieść do kwadratu, ale czy dobrze to zrobiłeś?
można tak
a
n=
√n2+2n−
√n2−2n=
| | (√n2+2n−√n2−2n)(√n2+2n+√n2−2n) | |
= |
| = |
| | √n2+2n+√n2−2n | |
| 4n | | 4n | |
| ≥ |
| = |
| √n2+2n+√n2−2n | | √n2+2n+1+√n2−2n+1 | |
19 kwi 22:14
Szkolniak: z rozpędu dwójki z prawej nie podniosłem do kwadratu

19 kwi 22:16
Saizou : 
19 kwi 22:17
Saizou :
Zadanie 5
Wykaż, że jeżeli funkcja kwadratowa f(x)=x
2+bx+c ma miejsce zerowe,
| | 1 | | 1 | |
to funkcja kwadratowa określona wzorem g(x)=x2+(m− |
| )bx+(m− |
| )2c, |
| | m | | m | |
gdzie m≠0, również ma miejsce zerowe.
19 kwi 22:20
Szkolniak: f(x)=x
2+bx+c
Δ=b
2−4c≥0 (z treści zadania)
Δ z g(x):
| | 1 | | 1 | | 1 | | 1 | |
Δ=(m− |
| )2b2−4c(m− |
| )2=(m− |
| )2(b2−4c)≥0, bo: b2−4c≥0 i (m− |
| )2≥0 |
| | m | | m | | m | | m | |
(każda liczba rzeczywista podniesiona do kwadratu jest liczną nieujemną)
19 kwi 22:27
f123: f(x) − miejsce zerowe ====> Δ = 0 = b
2 − 4c
g(x):
| | 1 | | 1 | | 1 | |
Δg = (m − |
| 2 * b2 − (m − |
| ) * c = (m − |
| )2(b2 − 4c) |
| | m | | m | | 2 | |
b
2 − 4c = 0 − czyli funkcja g(x) ma miejsce zerowe, bo Δ
g = 0
19 kwi 22:28
Saizou :
Szkolniak  Zadanie 6
Zadanie 6
Odcinek o końcach A=(6,0) i C=(2,8) jest przekątną rombu ABCD.
Pole tego rombu jest równe 40. Oblicz promień r okręgu wpisanego w ten romb
i napisz równanie tego okręgu.
19 kwi 22:32
f123: (x − 4)
2 + (y − 4)
2 = 10, r =
√10 
19 kwi 22:45
Godzio: f123 jest ok

20 kwi 02:04
Igor: Wewnątrz trójkąta równoramiennego prostokątnego ABC, (CAB=90o) wybrano punkt P tak ze AP=3,
BP=4 oraz CP=5. Oblicz pole ABC.
Kto pomoze?
20 kwi 08:21
Saizou :
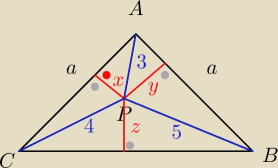
9=x
2+y
2
16=(a−y)
2+x
2
25=(a−x)
2+y
2
Stąd masz x oraz y w zależności od a.
Z równania 9=x
2+y
2 wyznaczysz a
2
20 kwi 11:48
Igor: Powoli

a skąd to 9=x
2+y
2 ?
20 kwi 12:06
Saizou :
ten prostokąt do góry, tam gdzie są 3, x, y
20 kwi 12:09
Igor: ok dziękś kapisz już

20 kwi 12:11
 Zad. 1
Przekątne trapezu ABCD przecinają się w punkcie M.
Wysokość trapezu ma długość 18.
Pole trójkąta ABM jest równe 25, pole trójkąta CDM jest równe 16.
Oblicz pole trapezu.
Zad. 1
Przekątne trapezu ABCD przecinają się w punkcie M.
Wysokość trapezu ma długość 18.
Pole trójkąta ABM jest równe 25, pole trójkąta CDM jest równe 16.
Oblicz pole trapezu.

 . Jakiś skrypt mnie nie przepuszcza na Safari.
(śmieszne bo tylko na MacBooku, a na Ipadzie normalnie idzie).
I robię za czarną oFcę
. Jakiś skrypt mnie nie przepuszcza na Safari.
(śmieszne bo tylko na MacBooku, a na Ipadzie normalnie idzie).
I robię za czarną oFcę 

 fil
fil
 Zadanie 2
Wysokość H prawidłowego ostrosłupa sześciokątnego jest dwa razy większa
niż długość a krawędzie jego podstawy.
Oblicz cosinus kąta zawartego między sąsiednimi ścianami bocznymi tego ostrosłupa.
Zadanie 2
Wysokość H prawidłowego ostrosłupa sześciokątnego jest dwa razy większa
niż długość a krawędzie jego podstawy.
Oblicz cosinus kąta zawartego między sąsiednimi ścianami bocznymi tego ostrosłupa.



 Zad 2
Pole jednego trojkata:
Zad 2
Pole jednego trojkata:


 Zadanie 4
Dany jest ciąg o wyrazie ogólnym an=√n2+2n−√n2−2n.
Wykaż, że an > 2 dla dowolnej liczby naturalnej n>1.
Zadanie 4
Dany jest ciąg o wyrazie ogólnym an=√n2+2n−√n2−2n.
Wykaż, że an > 2 dla dowolnej liczby naturalnej n>1.



 Zadanie 6
Odcinek o końcach A=(6,0) i C=(2,8) jest przekątną rombu ABCD.
Pole tego rombu jest równe 40. Oblicz promień r okręgu wpisanego w ten romb
i napisz równanie tego okręgu.
Zadanie 6
Odcinek o końcach A=(6,0) i C=(2,8) jest przekątną rombu ABCD.
Pole tego rombu jest równe 40. Oblicz promień r okręgu wpisanego w ten romb
i napisz równanie tego okręgu.


 9=x2+y2
16=(a−y)2+x2
25=(a−x)2+y2
Stąd masz x oraz y w zależności od a.
Z równania 9=x2+y2 wyznaczysz a2
9=x2+y2
16=(a−y)2+x2
25=(a−x)2+y2
Stąd masz x oraz y w zależności od a.
Z równania 9=x2+y2 wyznaczysz a2
 a skąd to 9=x2+y2 ?
a skąd to 9=x2+y2 ?
