Pytanie Szkolniak: Często w zadaniach spotykam się z sytuacją, że, załóżmy, muszę wyznaczyć 'a' za pomocą 'b' lub na odwrót, a 'utrudnioną' sprawą w tym jest to, że pojawiają się tam drugie i pierwsze potęgi. Przykładem niech będzie równanie z zadania robionego teraz: 4ab=√3(a²+b²) Przychodzą mi na myśl dwie metody aby wyznaczyć 'a': −dopełnienie do kwadratu zupełnego (co tutaj z moich obliczeń nie sprawdza się za dobrze) −potraktowanie tego jak zwykłe równanie kwadratowe ze względu na niewiadomą 'a' Pytanie czy są jeszcze inne metody, i po drugie − jaka jest najbardziej optymalna metoda?

Saizou : jet to równanie tzw. symetryczne √3a²−4ab+√3b²= 0. |:b²≠0 (gdy b=0, to a=0)

	a		a		a
√3(		)2+4		+√3=0. i podstawić		=t
	b		b		b

ale to sprowadza się do równania kwadratowego

Saizou : Wszystko zależy od tego jaką masz zależność podaną

Szkolniak: W sensie jaką zależność masz na myśli? Może przybliżę: mam za zadanie wyznaczyć kąty trójkąta prostokątnego i chcę wyznaczyć jedną niewiadomą zależną od drugiej abym mógł je skrócić korzystając z trygonometrii w trójkącie. Korzystając ze sposobu równania kwadratowego wychodzą mi dwa pierwiastki:

	√3
a1=		*b v a2=√3*b
	3

Rozumiem że mam rozpatrzeć dwa przypadki?

Saizou : Tak, chyba, że gdzieś założysz, że a>b. Lepiej podaj całą treść, bo tak można gdzieś strzelić gafę.

Szkolniak: Treść: Na przeciwprostokątnej AB trójkąta prostokątnego ABC zbudowano trójkąt równoboczny ABX. Wyznaczyć kąty trójkąta ABC jeżeli wiadomo, że pole trójkąta ABX jest dwa razy większe od pola trójkąta ABC. Wydaje mi się że nie ma tutaj żadnego ograniczenia

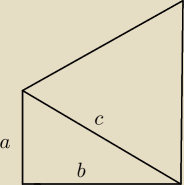
Saizou : Możesz założyć, że np. a < b (w tym zadaniu nic nie stracisz)

Szkolniak: Rzeczywiście, wyjdą po prostu odwrotne kąty, dzięki piękne

Saizou : Dokładnie