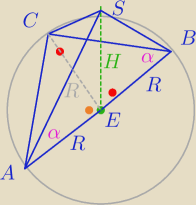
 Każda z krawędzi bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt α. Podstawą tego
ostrosłupa jest trójkąt prostokątny o przeciwprostokątnej 2c i kącie ostrym γ. Wyznacz objętość
tego ostrosłupa.
Gdyby rysunek był nieczytelny to |∡EBS|=α i tak samo |∡EAS|=α
Czy odcinek |CE| jest prostopadły do |AB| i upada na punkt E? Z twierdzenia o trzech prostych
prostopadłych wynika (chyba), że jest. Tj. |AB| ⊥ |SE| ⇔ |AB| ⊥ |CE| więc |CE| powinien być
prostopadły do |AB| i upadać na punkt E. Wtedy odcinek |CE| byłby wysokością podstawy, a gdy
tak jest wówczas po obliczeniach wychodzą złe wyniki zatem ten odcinek nie jest prostopadły do
|AB|. Moje pytanie: Dlaczego?
Byłbym wdzięczny za pomoc
Każda z krawędzi bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt α. Podstawą tego
ostrosłupa jest trójkąt prostokątny o przeciwprostokątnej 2c i kącie ostrym γ. Wyznacz objętość
tego ostrosłupa.
Gdyby rysunek był nieczytelny to |∡EBS|=α i tak samo |∡EAS|=α
Czy odcinek |CE| jest prostopadły do |AB| i upada na punkt E? Z twierdzenia o trzech prostych
prostopadłych wynika (chyba), że jest. Tj. |AB| ⊥ |SE| ⇔ |AB| ⊥ |CE| więc |CE| powinien być
prostopadły do |AB| i upadać na punkt E. Wtedy odcinek |CE| byłby wysokością podstawy, a gdy
tak jest wówczas po obliczeniach wychodzą złe wyniki zatem ten odcinek nie jest prostopadły do
|AB|. Moje pytanie: Dlaczego?
Byłbym wdzięczny za pomoc 
 To co napisałeś jest prawdą tylko w trójkącie prostokątnym równoramiennym.
To co napisałeś jest prawdą tylko w trójkącie prostokątnym równoramiennym.
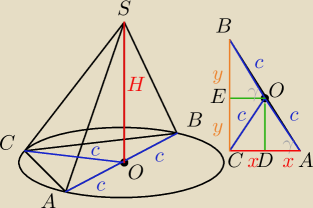
| H | ||
tgα= | ||
| c |
| x | ||
cosγ= | ||
| c |
| y | ||
sinγ= | ||
| c |
| 1 | 1 | |||
V= | * | *2x*2y*H =... | ||
| 3 | 2 |


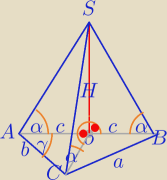 |∡ACB|=900
Każda z krawędzi bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt α⇔
spodek wysokości ostrosłupa leży w środku okręgu opisanego na podstawie ,
czyli w środku przeciwprostokątnej.
1) Płaszczyzna ABS jest prostopadła do płaszczyzny ABC.
Prosta SO jest prostopadła do pł. ABC i przebija ją w punkcie O,
to jest prostopadła do każdej prostej leżącej w pł. ABC i przechodzącej przez punkt przebicia.
W takim razie SO⊥AB i SO⊥OC. I koniec.
O położeniu CO w stosunku do AB nic Ci tw. nie mówi.
Oczywiście CO nie jest prostopadłe do AB , bo ΔABC nie jest równoramienny.
|AO|=|OB|=|OC|=c =R
Dalej licz sam, bo wiem, że potrafisz.
|∡ACB|=900
Każda z krawędzi bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt α⇔
spodek wysokości ostrosłupa leży w środku okręgu opisanego na podstawie ,
czyli w środku przeciwprostokątnej.
1) Płaszczyzna ABS jest prostopadła do płaszczyzny ABC.
Prosta SO jest prostopadła do pł. ABC i przebija ją w punkcie O,
to jest prostopadła do każdej prostej leżącej w pł. ABC i przechodzącej przez punkt przebicia.
W takim razie SO⊥AB i SO⊥OC. I koniec.
O położeniu CO w stosunku do AB nic Ci tw. nie mówi.
Oczywiście CO nie jest prostopadłe do AB , bo ΔABC nie jest równoramienny.
|AO|=|OB|=|OC|=c =R
Dalej licz sam, bo wiem, że potrafisz.
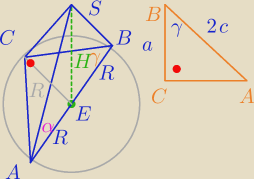 Rozwiązanie:
Krawędzie boczne pochylone są pod tym samym kątem do podstawy ostrosłupa zatem na
podstawie tego ostrosłupa można opisać okrąg, którego środkiem jest spodek wysokości.
Jeśli podstawą jest trójkąt prostokątny to środek okręg na nim opisanego leży na środku jego
przeciwprostokątnej zatem spodek wysokości ostrosłupa jest dokładnie na środku
przeciwprostokątnej |AB|.
|∡SEA| = |∡SEB| = 90o
|∡SAE| = |∡SBE| = α
|∡EBS| = γ
W podstawie:
|∡ACB| = 90o
|AB| = 2c ⇔ 2R = 2c ⇔ R = c
|AE| = |EB| = |CE| = R
Z funkcji trygonometrycznych dla ΔAES:
tgα = HR
tgα = Hc
H = c * tgα
Z funkcji trygonometrycznych dla △CAB (podstawa ostrosłupa):
cosγ = a2c
a = 2c * cosγ
Pp = 12 * a * 2c * sinγ = 12 * 2ccosγ * 2csinγ = c22sinγcosγ = c2sin2γ
V = 13 * c2sin2γ * c * tgα = 13 * c3sin2γtgα
Widocznie nadal nie bardzo rozumiem to twierdzenie o trzech prostych prostopadłych.
Rozwiązanie:
Krawędzie boczne pochylone są pod tym samym kątem do podstawy ostrosłupa zatem na
podstawie tego ostrosłupa można opisać okrąg, którego środkiem jest spodek wysokości.
Jeśli podstawą jest trójkąt prostokątny to środek okręg na nim opisanego leży na środku jego
przeciwprostokątnej zatem spodek wysokości ostrosłupa jest dokładnie na środku
przeciwprostokątnej |AB|.
|∡SEA| = |∡SEB| = 90o
|∡SAE| = |∡SBE| = α
|∡EBS| = γ
W podstawie:
|∡ACB| = 90o
|AB| = 2c ⇔ 2R = 2c ⇔ R = c
|AE| = |EB| = |CE| = R
Z funkcji trygonometrycznych dla ΔAES:
tgα = HR
tgα = Hc
H = c * tgα
Z funkcji trygonometrycznych dla △CAB (podstawa ostrosłupa):
cosγ = a2c
a = 2c * cosγ
Pp = 12 * a * 2c * sinγ = 12 * 2ccosγ * 2csinγ = c22sinγcosγ = c2sin2γ
V = 13 * c2sin2γ * c * tgα = 13 * c3sin2γtgα
Widocznie nadal nie bardzo rozumiem to twierdzenie o trzech prostych prostopadłych.  Myślałem, że działa ono w ten sposób, że:
Niech |AB| = m, |SE| = k', |CE| = k. Wtedy prosta m jest prostopadła do prostej k wtedy i tylko
wtedy gdy prosta m jest prostopadła również do prostej k'.
I myślałem, że prosta k i prosta k' mają punkt wspólny w postaci punktu E w tym przypadku.
Myślałem, że działa ono w ten sposób, że:
Niech |AB| = m, |SE| = k', |CE| = k. Wtedy prosta m jest prostopadła do prostej k wtedy i tylko
wtedy gdy prosta m jest prostopadła również do prostej k'.
I myślałem, że prosta k i prosta k' mają punkt wspólny w postaci punktu E w tym przypadku.
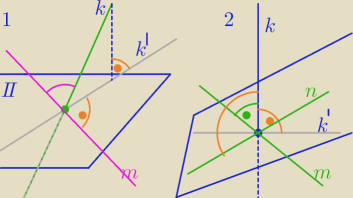 W tym zadaniu masz inną sytuację z prostopadłością niż w poprzednim zadaniu.
1) Poprzednio:
P− punkt przebicia płaszczyzny przez prostą k
k'− rzut prostokątny prostej k na płaszczyznę π
Prosta m jest prostopadła do prostej k, wtedy i tylko wtedy, gdy jest prostopadła do prostej
k'.
2)
Jeżeli prosta przebija płaszczyznę π i jest do niej prostopadła , to jest prostopadła
do każdej prostej leżącej w tej pł. i przechodzącej przez punkt przebicia P.
k⊥k'
k⊥m
k⊥n
W tym zadaniu masz inną sytuację z prostopadłością niż w poprzednim zadaniu.
1) Poprzednio:
P− punkt przebicia płaszczyzny przez prostą k
k'− rzut prostokątny prostej k na płaszczyznę π
Prosta m jest prostopadła do prostej k, wtedy i tylko wtedy, gdy jest prostopadła do prostej
k'.
2)
Jeżeli prosta przebija płaszczyznę π i jest do niej prostopadła , to jest prostopadła
do każdej prostej leżącej w tej pł. i przechodzącej przez punkt przebicia P.
k⊥k'
k⊥m
k⊥n

