trójkat matma: W trójkącie o bokach a,b,c poprowadzono dwusieczną kąta między bokami a i b Wyznacz stosunek odcinków,na jakie środek okręgu wpisanego w ten trójkąt dzieli odcinek tej dwusiecznej zawarty w tym trójkącie.

Leszek: Zrob rysunek , kat miedzy bokami a i b niech bedzie 2α Z trojkata prostokatnego : sin α = r/x , r − promien okregu , x dlugosc odcinka dwusiecznej od srodka okregu do wierzcholka miedzy bokami a i b

	r(a+b+c)
Na podstawie pola trojkata otrzymasz sin 2α =
	ab

Dokoncz

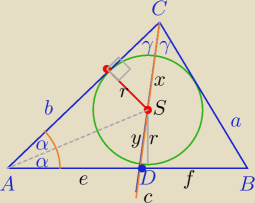
Mila: 1)

	1
PΔADS=		*|AD|*|AS|*sinα
	2

	1
PΔACS=		*|AS|* b*sinα
	2

x		1   *|AS|* b*sinα 2
	=
y		1   *|AD|*|AS|*sinα 2

x		b
	=
y		e

2) Z tw. o dwusiecznej kąta w trójkącie:

b		a
	=		i e+f=c
e		f

stąd:

	bc
e=
	a+b

3)

x		a+b
	=
y		c

Posprawdzaj obliczenia

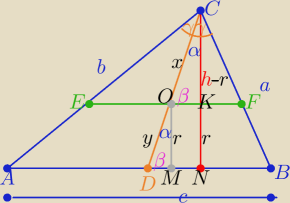
Eta: 2 sposób Z podobieństwa trójkątów DMO i CKO z cechy (kk)

x		h−r		x		h
	=		⇒ (*)		=		−1
y		r		y		r

hc

r(a+b+c)

h

a+b+c

h

a+b

P(ABC)=

i P(ABC)=

⇒

=

⇒

=

+1

2

2

r

c

r

c

	h
podstawiając za		do (*)
	r

	x		a+b
to		=
	y		c

=============