pole mira: Dany jest trójkąt ABC oraz jego pole P. Niech D bedzie środkiem odcinka BC.. Punkty X,Y,Z leżą odpowiednio na AB, AD, AC tak że AX = 2AB, AY = 3AD oraz AZ = 4AC. Oblicz pole trójkąta XYZ.

Saizou :

	1
P=		•2x•h=xh
	2

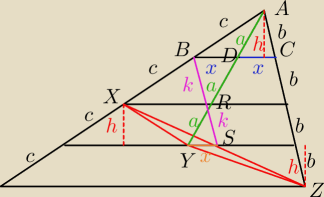
ΔYRS ≡ ΔDRB (b−k−b), zatem BD = YS =x

	1		1
PXYZ = PYZS + PYXS =		xh+		xh=xh=P
	2		2

mira: Mi kolega napisał że mu wyszło 2P

mira: Czemu te trzy h są takie same?

Saizou : Trójkąty są podobne, np. ΔBCA~ΔXRA w skali k=2 ⇒ wysokość trójkąta XRA jest równa 2h, czyli wysokość trapezu XPCB=h (P punkt przecięcia prostych XR i AC) itd.

Eta: Nawet 4 h takie same bo 4 b takie same

Saizou : Eta Prawda Coś logowanie mi nie działa i jestem czarną oFcą

mira: Czli odpowiedź to P nie 2P

Ula: To zadnie z kangura i wyszło 2P

Ula: Nie sorry jednak to nie to, to było inne zadanie