funkcja anonim123: f(x)=3x³−pix²+pi Jest większa od zera jak to rozwiązać Jeszcze nie wiem skąd tutaj https://forum.zadania.info/viewtopic.php?f=21&t=84781 w zadaniu 1 bierze się druga linijka postu Radagasa

: najlepiej zapytaj na tamtym forum

anonim123: A ktoś z tego forum mógłby to wytłumaczyć?

f123:

π		l2		l		3		r2		h
	<		*		==========		>		*
3		r2		h		π		h2		l

anonim123: f123 A skąd wziąłeś pierwszą nierówność w swoim poście?

anonim123: Już wiem

anonim123: A potem co należy zrobić aby skończyć to zadanie?

anonim123: Jak już mam funkcje sin²alfa*cosalfa?

anonim123: Może ktoś pomóc?

anonim123:

	3
Proszę o wytłumaczenie co należy zrobić po wyliczeniu że		>sin2alfa*cosalfa
	pi

ICSP:

	π
Pokazać, że ta nierówność jest prawdziwa dla dowolnego kąta 0 < α <
	2

anonim123: Niestety nie wiem jak to wykonać

ICSP:

	1		1		1		1
sin2xcosx =		sin(x)sin(2x) =		[cosx − cos(3x)] <		(1 + 1) =		<
	2		4		4		2

	3		3
		<
	6		π

Możesz tez pochodną.

ICSP: Wychodzę. Przeanalizuj to sobie bo jest tutaj trochę skrótów myślowych Jak rozpiszesz to zobaczysz wszystkie przekształcenia.

ICSP: i na końcu pierwszej linijki zamiast < powinno być =.

anonim123: pierwsze przekształcenie jest ze wzoru na iloczyn funkcji trygonometrycznych? Jeżeli tak to dlaczego we wzorze sin(alfa−beta) się nie równa sin0?

anonim123: Ok. Spróbuję to zrozumieć.

f123:

	1
@anonim123 sin2xcosx = sinxsinxcosx =		sinxsin2x
	2

anonim123:

	1
Jeszcze nie wiem co się stało tutaj		(1+1) Skąd te działania?
	4

f123: Chyba ze jest to mneijsze od wartosci maksymalnej tego wyrazenia po lewo

anonim123:

	1
Ale nie wiem dlaczego te wartości pojawiają się w nierówności tzn.		(1+1).
	4

anonim123: Czy muszę tam zastosować wzór na różnicę funkcji trygonometrycznych?

anonim123: ?

anonim123: Ktoś mógłby pomóc, bo nie rozumiem skąd to wynikło?

ICSP: cosx ≤ 1 −cos(3x) ≤ 1 zatem cosx − cos(3x) ≤ 2

anonim123: Dziękuję A jak z pochodną to zrobić?

ICSP: definiujesz sobie funkcję : f(x) = sin²(x)cos(x)

	π		3
i pokazujesz, że na przedziale (0		) jej maxima są mniejsze od
	2		π

anonim123: Czyli to by było tak f'(x)=cos²(x)[−sin(x)]? I co dalej?

ICSP: 1. Źle policzona pochodna 2. Na wyznaczanie ekstremów funkcji jest konkretny schemat. Liczysz pochodną: f' Rozwiązujesz równanie f'(x) = 0 Liczysz drugą pochodną lub obserwujesz zmianę znaku w otoczeniu punktów zerujących pochodną Wyciągasz wnioski o maximum i minimum. Wyznaczasz konkretne wartości. Jeżeli nie miałeś jeszcze pochodnych nie ma sensu abyś teraz ją wykorzystywał.

ICSP: W skrócie: Nie używaj "narzędzi" których jeszcze nie opanowałeś do rozwiązywania trudniejszych przykładów. Zacznij zabawę z ekstremami i pochodną od funkcji wielomianowych.

anonim123: Nie miałam i nie będę mieć uczę się sama. Jak powinno się policzyć tą pochodną?

ICSP: f'(x) = (sin²(x) cos(x) )' = (sin²(x))'cosx + sin²(x) * (cos(x))' = = 2sin(x)cos²(x) − sin³(x)

	π
teraz równanie f'(x) = 0 w przedziale (0 ,		)
	2

anonim123: czy skorzystałeś ze wzoru (f*g)'=f'g+fg'?

ICSP: tak i ze wzoru na pochodną złożenia w celu policzenia pochodnej sin²(x)

anonim123: A skąd jest w 2sin(x)cos²(x) cos²(x) bo kiedy próbuje podstawić do wzoru 20:10 to nie wiem dlaczego to tam jest

ICSP: [sin²(x)]' = 2sin(x)* (sinx)' = 2sin(x)cos(x)

anonim123: To już rozumiem A jak obliczyć f'(x) = 0 ?

ICSP: 2sin(x)cos²(x) − sin³(x) = 0 to jest zwykłe równanie trygonometryczne.

anonim123:

	1
To będzie tak 2*		(sinx+x+sin(x−x)*cos(x)−sin3(x)
	2

sin2x*cosx−sin³(x) Czy tutaj mam jakiś błąd?

anonim123: Nie bardzo wiem jak to obliczyć. Proszę o pomoc.

ICSP: 2sin(x)cos²(x) − sin³(x) = 0 2cos²(x) − sin²(x) = 0 3cos²(x) = 1

	1		√2
cos(x) =		⇒ sin(x) =
	√3		√3

	1
Pochodna w punkcie dla któego cos(x) =		zmienia znak z plusa na minus, więc znajduje
	√3

się tam maksimum równe

	1		√2		2
fmax =		* (		)2 =
	√3		√3		3√3

anonim123: Skąd mam wiedzieć że zmienia znak z plusa na minusa?

ICSP: Wykres lub Rozwiązanie nierówności f'(x) > 0 i f'(x) < 0 alternatywnym sposobem jest policzenie drugiej pochodnej i sprawdzenie czy

	1
f''(x) < 0 dla cosx =
	√3

anonim123: Nie wiem jak to mam zaznaczyć na wykresie.

ICSP:

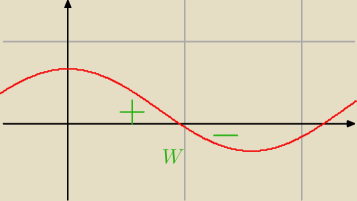
	1
Wykres funkcji f(x) = cos2(x) −
	3

Widać, że następuje tutaj zmiana z + na −. Naprawdę radzę zacząć od prostszych przykładów.

anonim123: A w jakich przypadkach trzeba używać pochodnej? f(x)=0 to miejsce zerowe ale dlaczego akurat w tym miejscu a nie dalej na wykresie?

anonim123: Oglądnęłam matemaksa, ale nie wiem jak poradzić sobie z tym zadaniem. Dlaczego miejsce zerowe W jest akurat w tym miejscu?

ICSP:

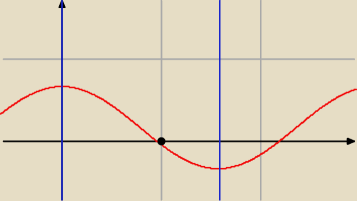
	π
Ponieważ musi znajdować się ono w przedziale (0 ;		)
	2

Zamieszczam wykres z zaznaczonym przedziałem (linie pionowe) Jedyne miejsce zerowe pomiędzy tymi liniami zostało oznaczone kropką.

anonim123: A dlaczego akurat taki przedział muszę wziąć pod uwagę?

anonim123: ?

ICSP: Gdyż kąt rozwarty stożka nie może być większy ani równy 180^o Przeanalizowałaś w ogóle to zadanie?

anonim123: Nie pomyślałam o tym.

gal nie anonim 321: a takie równanie: alfocosalfosinalfatanalfa to jak rozwiązac , bo ja nie myślę