Probablistyka Melka: Hej mogłabym prosić o podpowiedzi do takiego zadania Pacjent odwiedzający lekarza skarży się na objawy które w jednym na 100 przypadków towarzyszą chorobie nowotworowej. Lekarz wykonuje test krwi który potwierdza chorobę z prawdopodobieństwem 0,98 jeśli pacjent jest naprawdę chory. Test może także błędnie z prawdopodobieństwem 0,2 wskazać obecność nowotworu u osoby zdrowej. Jeżeli test wypadanie pozytywnie to jakie jest prawdopodobieństwo że badana osoba ma nowotwór

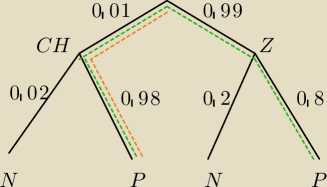
ite: Dobrym sposobem wyobrażenia sobie tego zagadnienia jest − przed zapisaniem rozwiązań − narysowanie drzewka. P − pozytywny wynik testu N − negatywny wynik testu P(P) − prawdopodobieństwo że test wypadł pozytywnie P(CH∩P) prawdopodobieństwo że badana osoba ma nowotwór i że jej test wypadł pozytywnie P(CH|P) prawdopodobieństwo że badana osoba ma nowotwór pod warunkiem, że test wypadł pozytywnie

Melka: Czyli P(CH|P) = U{0,01*0,98){0,01*0,98 + 0,99 * 0,8}

Melka:

	0,01*0,98
Czyli P(CH|P) =
	0,01*0,98 + 0,99 * 0,8

Melka: Czy dobrze?

ite: Na gałęzi drzewka Z→ P błędnie zapisałam 0,8, powinno być 0,2 (Test może także błędnie z prawdopodobieństwem 0,2n wskazać obecność nowotworu u osoby zdrowej.) Rozwiązanie jest prawidłowe, jeśli w mianowniku zapisać 0,01*0,98 + 0,99 * 0,2 to i wynik będzie poprawny.

Melka: Czyli wynik ~4,7 Bardzo dziękuje za pomoc

ite: prawdopodobieństwo nie może tyle wynosić

ite: przecinek w innym miejscu ~0,047

Melka: Chodziło mi procentowo nie jasno napisałam