dowod f123: Uzasadnij ze dla dowlonych liczb rzeczywistych x i y prawdziwa jest nierownosc: (x + 1)(x + 2) + (y + 1)(y + 2) + 1 >= (x + 2)(y + 2)

f123: b

mira: (x − y)² +1 ≥ −x−y

f123: mira a gdzie sie podzialo "xy"

Saizou : metodą PW y=kx dla k≠0 (x+1)(x+2)+(kx+1)(kx+2)+1 ≥ (x+2)(kx+2) x²+3x+2+k²x²+3kx+2+1 ≥ kx²+2x+2kx+4 (1−k+k²)x²+(1+k)x+1 ≥ 0 (*) pokażemy, że ta nierówność jest spełniona dla każdego x oraz k≠0 Δ=(1+k)²−4(1−k+k²)=k²+2k+1−4+4k−4k²=−3k²+6k−3=−3(k²−2k+1)=−3(k−1)² ≤ 0 oraz 1−k+k² > 0, zatem nierówność (*) jest spełniona dla każdego x i k≠0. Dla k =0 mamy x=y=0, stąd wyjściowa nierówność wygląda następująco 2+2+1 ≥ 2+2 co jest prawdą. Zatem prawdziwa jest nierówność (x+1)(x+2)+(y+1)(y+2)+1 ≥ (x+2)(y+2) cud

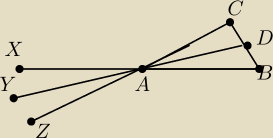
mira: sory a ktoś umie to: Dany jest trójkąt ABC oraz jego pole P. Niech D bedzie środkiem odcinka BC.. Punkty X,Y,Z leżą odpowiednio na AB, AD, AC tak że AX = 2AB, AY = 3AD oraz AZ = 4AC. Oblicz pole trójkąta XYZ.

f123: @Saizou a po co podstawienie y = kx? Nie mozemy od razu potraktowac 'y' jako parametr?

xyz: x² + 3x + 2 + y² + 3y + 2 + 1 ≥ xy + 2x + 2y + 4 x² + 3x + 2 + y² + 3y + 2 + 1 − xy − 2x − 2y − 4 ≥ 0 x² − xy + y² + 3x + 3y + 1 − 2x −2y ≥ 0 x² − xy + y² + x + y + 1 ≥ 0 (x−y)² + xy + x + y + 1 ≥ 0 (x−y)² + x(y + 1) + y + 1 ≥ 0 (x−y)² + (y+1)(x+1) ≥ 0 wiadomo ze (x−y)² ≥ 0 dla dowolnego x,y ∊ ℛ pytanie co z wyrazeniem (x+1)(y+1) ?

f123: nic

mira:

	y−1		3(y−1)2
(x−		)2+		≥0
	2		4

Saizou : (x + 1)(x + 2) + (y + 1)(y + 2) + 1 >= (x + 2)(y + 2) x²+y²+x+y+1−xy ≥ 0 /*2 x²+2x+1+y²+2y+x²−2xy+y² ≥ 0 (x+1)² + (y+1)²+(x−y)² ≥ 0 + komentarz

mira: