planimetria
jaros:
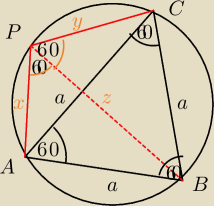
Dany jest trójkąt równoboczny ABC wpisany w okrąg. Punkt P leży na krótszym łuku AC. Wykaż, że
|PB|=|PA|+|PC|.
Wiemy, że kąt IAPBI = 60, bo jest to kąt wpisany oparty na łuku AB tak samo jak kąt IACBI i
podobnie w przypadku kąta IBPCI
lecz co dalej

17 kwi 20:04
Leszek: Z twierdzenia sinusow .
17 kwi 20:08
jaros: że z2 z jednego to to samo co z2 z 2?
17 kwi 20:10
PW: Jakiś zamęt wprowadzasz. Co tu jest dane, a co jest Twoim rozumowaniem?
17 kwi 20:12
Leszek: Czy z to srednica okregu ? ?
17 kwi 20:12
f123: x = y
kat PAB = 90
Trojkat PAB 30, 60, 90
|PB| = 2 * x = x + y
17 kwi 20:38
Eta:
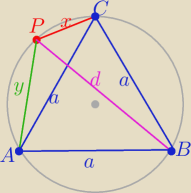
Łuki mają tę samą długość !
Z tw. Ptolemeusza
a*d=x*a+y*a /:a
d=x+y
|PB|=|PA|+|PC|
============
i po ptokach

17 kwi 20:46
jaros: Znaczy z to jest odcinek IPBI dlatego na ten odcinek chciałem stworzyć tw cos
17 kwi 20:53
jaros: Dziękuję Eta lecz chciałbym jeszcze zrobić sposób z tw cos
17 kwi 20:53
f123: @jaros z tw cosinusow wynika, z x = y i ze kat PAB = 90
17 kwi 20:56
f123: tak wlasciwie ze PAB = 90 to wynika pozniej
17 kwi 20:58
Eta:
1/ |∡CPB|=60o ( bo oparty na łuku BC
i |∡APB|=60o
i z tw. kosinusów
a2=x2+d2−xd i a2= y2+d2−yd
zatem
x2−y2= d(x−y)
(x−y)(x+y)=d(x−y)
d= x+y
c.n.w.
17 kwi 21:05
jaros: Dziękuje pięknie
17 kwi 21:10
 Dany jest trójkąt równoboczny ABC wpisany w okrąg. Punkt P leży na krótszym łuku AC. Wykaż, że
|PB|=|PA|+|PC|.
Wiemy, że kąt IAPBI = 60, bo jest to kąt wpisany oparty na łuku AB tak samo jak kąt IACBI i
podobnie w przypadku kąta IBPCI
lecz co dalej
Dany jest trójkąt równoboczny ABC wpisany w okrąg. Punkt P leży na krótszym łuku AC. Wykaż, że
|PB|=|PA|+|PC|.
Wiemy, że kąt IAPBI = 60, bo jest to kąt wpisany oparty na łuku AB tak samo jak kąt IACBI i
podobnie w przypadku kąta IBPCI
lecz co dalej
 Łuki mają tę samą długość !
Z tw. Ptolemeusza
a*d=x*a+y*a /:a
d=x+y
|PB|=|PA|+|PC|
============
i po ptokach
Łuki mają tę samą długość !
Z tw. Ptolemeusza
a*d=x*a+y*a /:a
d=x+y
|PB|=|PA|+|PC|
============
i po ptokach 