Styczna do wykresu/pochodna Jokur: Proste k i l przecinaja sie w pkt a=(4,0) oblicz pole trojkata abc gdzie b i c sa punktami stycznosci prostych k i l z wykresem funkcji f(x)=−x²−9

Jokur: Proszę o pomoc w rozwiązaniu, nie za bardzo wiem jak się do tego zabrać

wredulus_pospolitus: Krok 1: wyznaczasz ogólną postać stycznej zależną od parametru x₀ Krok 2: wyliczasz dla jakich x₀ styczne przechodzą przez punkt A Krok 3: to są pierwsze współrzędne punktów styczności ... wyznaczasz drugie współrzędne tych punktów styczności Krok 4: masz współrzędne wierzchołków trójkąta −−−− obliczasz jego pole

Jokur: dla stycznej: y=ax+b po podstawieniu pkt A otrzymałem y=ax−4a nastepnie wyznaczyłem a jako pochodną f(x) a=−2x, wyznaczyłem b=−4a=f(x_o)−f '(x_o)*x_o I właśnie w tym miejscu się zatrzymałem i nie mam pomysłu co z tym dalej zrobic

wredulus_pospolitus: f'(x_o) = ... ile

wredulus_pospolitus: f(x₀) = ... ile

Jokur: Niestety, nie wiem co mam z tym dalej zrobić i nie mam zbytnio pojęcia jak to wyliczyć

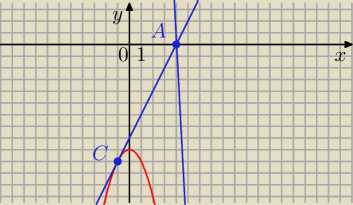
janek191: A = ( 4, 0) y = − x² − 9 y = a x + b 0 = 4a + b ⇒ b = − 4a y = ax − 4 a − x² − 9 = a x − 4a x² + a x − 4a + 9 = 0 Δ = a² − 4*(−4a + 9) = a² + 16 a − 36 = 0 Δ₁ = 256 − 4*1*(−36) = 256 + 144 = 400 √Δ₁ = 20

	−16 − 20		−16 + 20
a=		= −18 lub a =		= 2
	2		2

więc b = 72 lub b = − 8 y = − 18 x + 72 lub y = 2 x − 8 − x² − 9 = − 18 x + 72 x² − 18 x + 81 = 0 Δ₂ = 324 − 324 = 0

	18
x =		= 9
	2

y = − 90 B = ( 9, −90) − x² − 9 = 2 x − 8 x² + 2 x + 1 = 0 ( x + 1)² = 0 x = − 1 y = 2*(−1) − 8 = −10 C = ( − 1, − 10) Mamy A = ( 4, 0) B = ( 9, −90) C = ( − 1, − 10)

Jokur: Dziękuję bardzo Panie Janku za pomoc, niemniej jednak chciałbym zrozumieć rozwiązanie za pomocą pochodnych i jakby mógł je ktoś przedstawić

janek191: y ' = − 2 x więc ponieważ a = − 18 lub a = 2 mamy −2 x = − 18 lub −2 x = 2 x = 9 lub x = − 1 zatem y = −81 − 9 = −90 lub y = − 1 − 9 = − 10 czyli B = ( 9, − 90) C = ( − 1, − 10) =================================

wredulus_pospolitus: Krok 1: y = f'(x_o)(x − x_o) + f(x_o) y = −2x_o(x − x_o) + (−x_o² − 9) y = −2x_o*x + x_o² − 9 Krok 2: podstawiamy współrzędne punktu A 0 = −8x_o + x_o² − 9 −−> 0 = (x_o − 9)(x_o + 1) −−−> x_o = 9 lub x_o = −1 Krok 3: wyznaczamy drugie współrzędne itd.

Jokur: Dziękuję wam bardzo, jesteście wielcy!

wredulus_pospolitus: a wracając do tego co Ty miałeś: −4a=f(x_o)−f '(x_o)*x_o −−−> −4a = (−x_o² − 9) +2x_o² −−−> −4a = x_o² − 9 natomiast wiemy, że styczna ma mieć postać: y = ax −4a gdzie a = f'(x_o) = −2x_o stąd: −4*(−2x_o) = x_o² − 9 i masz to samo równanie kwadratowe

Jokur: Właśnie teraz zauważyłem, że miałem to samo i wystarczyło tylko zamienic x na x_o. Dostałem jakiegoś zaćmienia mózgu i nie wiedziałem co z tym zrobić. Ale no w końcu się udało, dziękuję wam raz jeszcze