Geometria analityczna FUITP: Punkty B = (0, 0) i D = (4, 2) są wierzchołkami kątów rozwartych rombu ABCD. Napisz równanie okręgu wpisanego w ten romb wiedząc, że kąt ostry rombu ma miarę 60 stopni. Teraz tak: środek okregu to S(2, 1). Skąd teraz promień? W internecie znalazłem informacje że trójkąt ABD jest równoboczny co się zgadza, i że połowa jego wysokości to będzie własnie promień, ale z czego to wynika? I jakie są jeszcze sposoby żeby to obliczyć?

FUITP: Dobra już wiem skąd ten promień, ale czy są inne sposoby?

ite: Zauważ, że odcinek BD należy do dwusiecznych kątów rozwartych rombu.

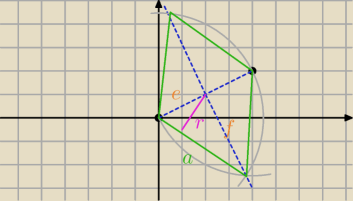
aniabb: r=e•f/a

aniabb: no i a=2e

aniabb: więc stąd r=f/2 czyli połowa wysokości

FUITP: Tak, już do tego doszedłem. Ale czy da się to rozwiązać w inny sposób niż połowa wysokości?

aniabb: np że Pole= połowa obwodu • r