tryg
jaros: 2sin(x)[cos(x) − sin(x)] ≥ 0
Ktoś mi to przedstawi co i jak zrobić?
17 kwi 13:50
Maciess:
2sinxcosx−2sin
2x≥0
| | 1 | | 1 | |
sin2x−2(− |
| cos2x+ |
| )≥0 |
| | 2 | | 2 | |
sin2x+cos2x≥1
| | 1 | | 1 | |
I tu powinno być łatwiej. Zastosowalem tożsamość sin2x=− |
| cos2x+ |
| |
| | 2 | | 2 | |
17 kwi 14:02
Jerzy:
2sinxcosx − 2sin2x ≥ 0 ⇔ sin2x + cos2x − 1 ≥ 0 ⇔ sin2x + cos2x ≥ 1
⇔ √2sin(π/4 − 2x) ≥ 1
17 kwi 14:08
Jerzy:
W nawiasie: (π/4 + 2x)
17 kwi 14:12
jaros: a co tam jest suma sinusa czy jak?
17 kwi 14:23
Jerzy:
cos2x = 1 − 2sin2x ⇔ − sin2x = cos2x − 1
17 kwi 14:27
jaros: znaczy mi chodzi o sin2x + cos2x i przeksztalcenie na (π/4 + 2x)
17 kwi 14:28
Jerzy:
Jest wzór, który można wyprowadzić , ale dobrze go zapamietać: sinx + cosx = √2sin(π/4 + x)
17 kwi 14:32
Jerzy:
14:27 −2sin2x = cos2x − 1 oczywiście
17 kwi 14:36
jaros: mogę go stosować na maturze?
17 kwi 14:42
Jerzy:
Tego nie wiem

17 kwi 14:44
WhiskeyTaster: Na maturze możesz korzystać ze wszystkiego, co jest prawdziwe. Nieważne, czy potrafisz tego
dowieść. Nikt nie oczekuje dowodu każdego twierdzenia, które nie znalazło się w tablicach
matematycznych.
17 kwi 14:45
WhiskeyTaster: Jerzy, a czemu nie? Przecież gdyby dowodzić wszystkiego, z czego się korzysta, to czasu by
zabrakło. Przecież równie dobrze jakiś układ równań można rozwiązać przy pomocy macierzy. I
wątpię, że będą wymagali dowodu, że sposób jest poprawny

17 kwi 14:48
Jerzy:
Na mojej maturze wszystko trzeba było mieć w głowie. Żadnych tablic i kalkulatorów

17 kwi 14:51
jaros: Umie ktos to mi przedstawić graficznie? byłbym dogzgonnie wdzieczny
17 kwi 15:11
jaros: mam pomysł na zrobnie czegos takiego sin(x) ≥ 0 cos(x) − sin(x) ≥ 0
1) raczej prosta
2) sin(x) ≥ cos(x)
tg(x) ≥ 0
i no jescze sprawdzenie czegos z cos(x) = 0
17 kwi 15:13
Jerzy:
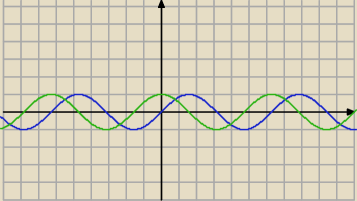
17 kwi 15:25
jaros: i co dalej jak mamy różnice?
17 kwi 15:44
Jerzy:
Ustalasz w jakich przedziałach niebieska krzywa ( sinx) leży nad zieloną ( cosx)
17 kwi 15:53
jaros: a da się to rozwoązać z tej neruwnosci co napisałem?
17 kwi 16:16



