odcinek Edyta: Wewnątrz trójkąta ABC o bokach BC = 3, CA = 5,AB = 6 wybrano punkt M. Z punktu M poprowadzono prostopadłe MA', MB', MC' odpowiednio do wysokości AD, BE, CF tak że AA' = BB'= CC'. Oblicz długość AA'.

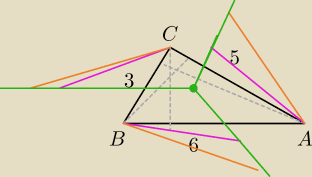
aniabb: np różowa albo pomaraczowa albo narysuj jeszcze kilka o innych długościach

Edyta: Ale co zauważyć na tych rysunkach?

aniabb: zielony punkt to M a A' może być gdzieś na zielonej linii więc szukana długość jest dość dowolna

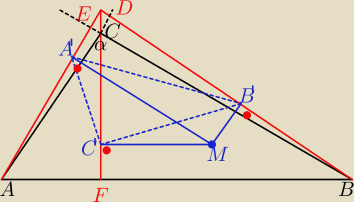
an: α>90^o AA'BB'=CC'≈2.3

Edyta:

	√56
Ja mam w odpowiedziach że 2*		, więc chyba da się to jakoś policzyć.
	7

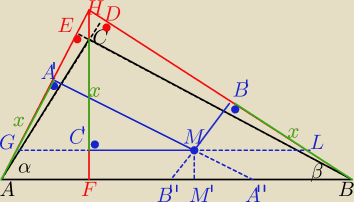
an: Wynik jest dokładnie jak podałaś mój podany wyżej zamiast x=CC'policzyłem dla x=CH Popatrz na zależności pomiędzy kątami np CAB i ABD to jest jeden z kluczy, ten rysunek choć pozwala stosunkowo proste rozwiązanie tego zadania, choć eta pewno uzna to za bohomaz.

Edyta: Jakoś tego niestety nie widze

an: Kąt ∡CAB=α ∡ADB=? mamy trójkąt ADB (suma kątówt =) to ABD = Następnie zastanów się jak wyliczyć wysokość CF. Dobranoc.

an: Rozwiązałaś czy czekasz na gotowca.

abx: No cóż , rozwiązania Ety są zrozumiałe, a przynajmniej wiadomo o co zapytać.

an: A o co chcesz zapytać, ja zadałem proste pytanie, czy nie potrafisz na nie odpowiedzieć ode mnie rozwiązania nie dostaniesz, bo to nie uczciwe, chociaż mogę podać ostatni wzór

	6*CF		4√14
x=		=
	7		7

Edyta: abx to nie ja