Dla Szkolniaka Saizou : Szkolniak to też zadanie od Ety z dawnych czasów. W trapezie o kątach ostrych 30^o i 60^o różnica kwadratów przekątnych trapezu wynosi 16 Oblicz pole tego trapezu.

Szkolniak: W zasadzie ten sam trik co w ostatnim zadaniu

Saizou : Jeśli chodzi o dorysowanie trójkąta, to tak.

Edyta: Czy 4√3?

Tadeusz: To podrzucę jeszcze takie (matura angielska lata sześćdziesiąte ubiegłego wieku) "Prostokątną kartkę o bokach a i b zgięto po przekątnej AC tak, że powstał kąt dwuścienny o mierze 60^o. Policz odległość punktów B i D"

Saizou : Tak, 4√3

	√a2+b2
Tadeusz czy to
	2

Bogdan: Przepraszam Saizou, ale pierwszy raz to ja zamieściłem to zadanie wiele lat temu na forum, potem to zadanie jeszcze kilka razy pojawiło się tutaj. Najciekawszy jest sposób rozwiązania tego zadania, Proszę rozwiązujących o pokazanie swoich rozwiązań.

Saizou : Bogdan ja nie twierdzę, że nie Sknociłem, bo narysowałem sobie kwadrat

Eta:

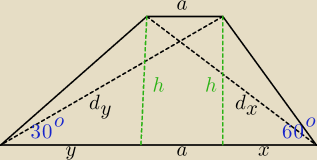
ite: ad. 11:42 sposób nienajkrótszy

	a+y+a+x
P=		*h
	2

h
	=√3 → x=h/√3
x

h
	=1/√3 → y=h√3
y

d_y²−d_x²= [h²+(y+a)²]−[h²+(x+a)²]= (y+a)²−(x+a)²=(y+2a+x)(y−x)=16 →y+2a+x=16/(y−x)

	16		√3
P=		*h= 8*
	2(y−x)		3−1

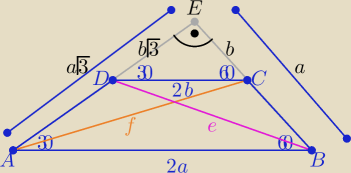
Eta: Oznaczenia na rys. "trójkąty ekierki" o kątach 30^o ,60^o, 90^o z tw. Pitagorasa f²=3a²+b² e²=a²+3b² − −−−−−−−− f²−e²= 2(a²−b²) ⇒ a²−b²=8 P(trapezu)= P(ABE)−P(DCE)

	a2√3		b2√3		√3
P=		−		=		(a2−b2)
	2		2		2

P=4√3 ======

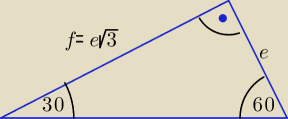
Bogdan: W tym zadaniu wartość pola powierzchni nie zależy od długości podstaw trapezu, można skracać jedną z podstaw co powoduje wydłużenie drugiej podstawy. Przyjmijmy więc, że górna podstawa ma długość równą 0, wtedy nasz trapez staje się trójkątem prostokątnym, a jego przekątne: e, f są przyprostokątnymi tego trójkąta.

	1
f2 − e2 = a ⇒ 3e2 − e2 = a ⇒ e2 =		a
	2

	1		1
Pole P =		e*e√3 =		a√3,
	2		4

	√3
w tym przykładzie a = 16, więc P =		*16 = 4√3
	4

Edyta: Zad Wewnątrz trójkąta ABC o bokach BC = 3, CA = 5,AB = 6 wybrano punkt M. Z punktu M poprowadzono prostopadłe MA', MB', MC' odpowiednio do wysokości AD, BE, CF tak że AA' = BB'= CC'. Oblicz długość AA'.

Bogdan: Pierwszy raz to zadanie zobaczyłem mając 17 lat, jeden z moich nauczycieli zaproponował mojej klasie, której wtedy bylem uczniem, rozwiązanie tego zadania i obiecał podwyższenie końcowej oceny każdemu, kto rozwiąże zadanie.

Bogdan: Edyto, załóż nowy wątek ze swoim zadaniem

Edyta: Jest ale nikt nie umie go rozwiązaa

Eta: Mój sposób rozwiązania też jest krótki