równanie
anonim123: dla jakich wartości parametru m rownanie −x2+3x+|x−4|=m ma jedno rozwiązanie? Mi wyszło m=5
z −x2+3x−x+4=m i m=0 gdy −x2+3x+x−4=m
16 kwi 16:15
wredulus_pospolitus:
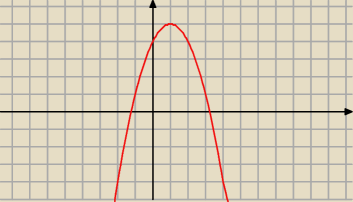
16 kwi 16:24
anonim123: A co gdy m=0 czy to jest właściwa odpowiedź? Gdy opuszczę wartość bezwzględną
16 kwi 16:29
WhiskeyTaster: −x2 + 3x + x − 4 = 0 dla x ≥ 4
−(x2 − 4x + 4) = 0
(x − 2)2 = 0
Wobec tego jedyne rozwiązanie to x = 2. Ale z założenia x ≥ 4.
Pamiętaj o założeniach!
16 kwi 16:37
wredulus_pospolitus:
nie jest ... bo dla m=0 masz także rozwiązanie w równaniu "−x2+3x−x+4=m"
16 kwi 16:37
anonim123: nie bardzo rozumiem dlaczego wynik m=0 jest zły

16 kwi 16:41
anonim123: Dlaczego są takie założenia?
16 kwi 16:42
wredulus_pospolitus:
dla m=0
masz:
dla x < 4 :
−x
2+3x−x+4=0 −−−> −x
2 + 2x + 4 = 0 −−−> masz dwa rozwiązania (okolice x = −1 oraz x = 3)
dla x ≥ 4
−x
2+3x+x−4=0 −−−> −x
2 + 4x − 4 = 0 −−−> nie masz W OGÓLE rozwiązań

(bo z równania
wyjdzie rozwiązanie dla x = 2 KTÓRY NIE JEST W PRZEDZIALE: x≥4

)
16 kwi 16:45
anonim123: aha dziękuję

16 kwi 16:46
WhiskeyTaster: Anonim, powiedz mi jedno: w jaki sposób rozwiązywałeś zadanie, skoro nie stosowałeś żadnych
założeń?
16 kwi 17:32


 (bo z równania
wyjdzie rozwiązanie dla x = 2 KTÓRY NIE JEST W PRZEDZIALE: x≥4
(bo z równania
wyjdzie rozwiązanie dla x = 2 KTÓRY NIE JEST W PRZEDZIALE: x≥4  )
)
