Geometria analityczna
Esssssa: Zad.1 Punkty A = (5,4), B = ( −1, 3) i C = (x , −1) są współliniowe. Wyznacz x .
Zad.2 Punkty A = (2,3), B = (6 , 5) i C ( −4 , 15) są wierzchołkami trójkąta. Prosta
zawierająca wysokość tego trójkąta poprowadzona z wierzchołka C przecina prosta AB
w punkcie D. Oblicz długość odcinka BD.
Zad.3 Dane są wierzchołki trójkąta ABC: A = (−2, 2) B = (8 , 7) i C = (3 , 9). Z
wierzchołka C poprowadzono wysokość tego trójkąta, która przecina bok AB w punkcie
D. Wyznacz równanie prostej przechodzącej przez punkt D i równoległej do boku BC.
Zad.4 Punkty A = (0,3) i B = (4 , 5) są wierzchołkami trójkąta równoramiennego ABC,
w którym |AB|=|BC| . Wysokość BD trójkąta zawiera się w prostej o równaniu
3x − y − 7 = 0. Oblicz:
a) współrzędne wierzchołka C
b) pole trójkąta ABC
Bardzo proszę o jakiekolwiek wskazówki, czy też rozwiązania. Proszę was

!
16 kwi 01:28
wredulus_pospolitus:
1)
krok 1 −−− tworzysz prostą zawierającą A i B
krok 2 −−− podstawiasz współrzędne punktu C do wzoru tejże prostej i sprawdzasz dla jakiego
'−x' spełnione jest równanie prostej
16 kwi 01:31
aniabb: tablice maturalne str 5

16 kwi 01:32
wredulus_pospolitus:
2)
krok 1 −−− wyznaczasz prostą przechodzącą przez punkty A i B
krok 2 −−− wyznaczasz prostą prostopadłą do prostej (1) przechodzącą przez punkt C
krok 3 −−− wyznaczasz punkt przecięcia się tychże prostych (jest to punkt D)
krok 4 −−− wyznaczasz długość odcinka |DB| (masz do tego odpowiedni wzór)
16 kwi 01:33
wredulus_pospolitus:
3)
krok 1−3 jak w poprzednim
krok 4 −−− wyznaczasz równanie prostej zawierającej punkty B i C
krok 5 −−− wyznaczasz równanie prostej równoległej do (4) i przechodzącej przez punkt D
16 kwi 01:34
aniabb:
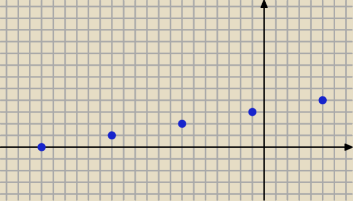
zabrakło mi kratek ale x=−25
16 kwi 01:35
wredulus_pospolitus:
4)
krok 1 −−− wyznaczasz prostą prostopadłą do podanej w zadaniu prostej i przechodzącą przez
punkt A
krok 2 −−− wyznaczasz punkt przecięcia się tychże prostych (punkt D)
krok 3 −−− wyznaczasz współrzędne punktu C mając:
I. współrzędne punktu A
II. współrzędne punktu D
III. wiedząc, że punkt D jest środkiem odcinka AC (odpowiedni wzór wykorzystaj
Obliczanie pola:
wyznacz |AC| oraz |BD| −−−− podstaw do wzoru na pole trójkąta.
16 kwi 01:38
wredulus_pospolitus:
Reszta zależy już tylko od Ciebie Essssa.
16 kwi 01:38
aniabb:
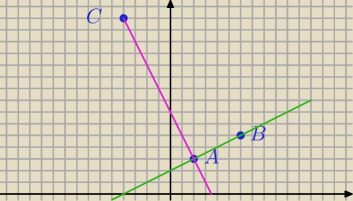
D=A więc BD=2
√5
16 kwi 01:40
aniabb:
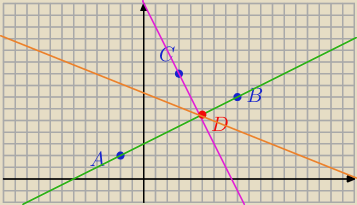
y=−0,4(x−4.8)+5.4
16 kwi 01:48
aniabb:
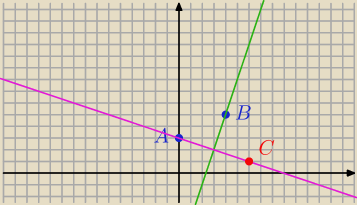
C=(6,1)
Pole=10
Wzór na pole np z tablic str 6 (wstawiasz tylko współrzędne punktów i masz wynik )
albo tak jak ja liczysz kratki

16 kwi 01:55
 !
!

 zabrakło mi kratek ale x=−25
zabrakło mi kratek ale x=−25
 D=A więc BD=2√5
D=A więc BD=2√5
 y=−0,4(x−4.8)+5.4
y=−0,4(x−4.8)+5.4
 C=(6,1)
Pole=10
Wzór na pole np z tablic str 6 (wstawiasz tylko współrzędne punktów i masz wynik )
albo tak jak ja liczysz kratki
C=(6,1)
Pole=10
Wzór na pole np z tablic str 6 (wstawiasz tylko współrzędne punktów i masz wynik )
albo tak jak ja liczysz kratki 