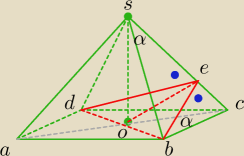
Podobieństwo trójkątów w ostrosłupie przy kącie dwuściennym Shizzer: |∡DEB| jest kątem dwuściennym. Wiem ze wskazówki do zadania, że |∡ESO| = |∡EBC| (oznaczyłem je na rysunku jako α) Więc z cechy KKK te trójkąty przeze mnie wypisane są podobne. Jednak niestety nie widzę w ogóle tej równości między kątami |∡ESO| i |∡EBC|. Mógłby mi ktoś napisać albo rozrysować lepiej z czego to wynika? (jeśli się da oczywiście) Byłbym wdzięczny za pomoc, wiele by mi to rozjaśniło w kwestii rozwiązywania zadań z kątami dwuściennymi

Saizou : Masz jakieś dane w tym zadaniu?

Shizzer: Przepraszam od razu, bo poprzednio źle kąty oznaczyłem Poprawnie powinno być: |∡COE|=|∡OSE|, czyli kąt nachylenia płaszczyzny wyznaczającej kąt dwuścienny do płaszczyzny podstawy i kąt między wysokością, a krawędzią boczną ostrosłupa. W tym zadaniu oznaczonego w książce jako zadanie z podstawy został ten fakt wykorzystany: Oblicz objętość ostrosłupa prawidłowego czworokątnego mając długość krawędzi podstawy 6 i miarę 120^o kąta między dwoma sąsiednimi ścianami bocznymi. Autor napisał, że posługując się rozwiązaniem zadania, którego treść napisałem powyżej można rozwiązać zadanie, nad którym myślę: Oblicz objętość ostrosłupa prawidłowego czworokątnego mając długość krawędzi podstawy a i miarę 2α kąta między sąsiednimi ścianami bocznymi. W rozwiązaniu pierwszego zadania został wykorzystany właśnie fakt, że ΔOCE~ΔOES z cechy KKK, ponieważ są prostokątne (to wiem) i |∡COE|=|∡OSE|. Tego co zaznaczyłem na czerwono nie rozumiem i chciałbym widzieć dlaczego i jakim sposobem te kąty są równe, bo ten fakt myślę, że będzie mi służył przy rozwiązywaniu tego typu zadań.

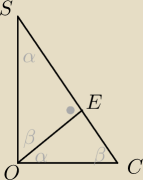
Saizou : a teraz widzisz to podobieństwo?

Shizzer: Z tego to podobieństwo wynika, że: α + β = 90^o To skoro kąt EOC=α i kąt CEO=90^o to ECO=β I podobnie uzupełniam kąty w trójkącie OSE?

Saizou : Tak To warto znać, bo często przewija się ten motyw w zadaniach.

Shizzer: Dziękuję za pomoc