Dowód planimetria
Szew: Dany jest kwadrat ABCD o środku w punkcie S i punkt P (poza kwadratem).
Udowodnij, że suma kwadratów odległości punktu P od wierzchołków A, B, C, D jest równa
4|𝑃𝑆|2 + |𝐴𝐶|2.
Nie wiem jak zabrać się za to zadanie, rysunek przypomina mi ostrosłup czworokątny.
15 kwi 22:13
Mila:
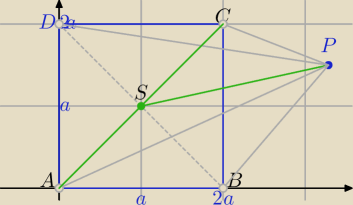
P=(x,y), S=(a,a)
A=(0,0), B=(2a,0), C=(2a,2a), D=(0,2a)
1) |AC|=2a
√2, |AC|
2=8a
2,
|PS|
2=(a−x)
2+(a−y)
2=a
2−2ax+x
2+a
2−2ay+y
2=x
2+y
2+2a
2−2a(x+y)
2)
|AP|
2=x
2+y
2
|BP|
2=(x−2a)
2+y
2
|CP|
2=(x−2a)
2+(y−2a)
2
|DP|
2=x
2+(y−2a)
2
3)
Suma kwadratów odległości od wierzchołków
S
k=2x
2+2(x−2a)
2+2*(y−2a)
2+y
2=
=4x
2+4y
2+12a
2−8a*(x+y)
4) S=4|PS|
2+|AC|
2=4*[x
2+y
2+2a
2−2a(x+y)]+8a
2=
=4x
2+4y
2+8a
2−8a(x+y)+8a
2=
=4x
2+4y
2+12a
2−8a(x+y)⇔
S
k=S
cnw
Posprawdzaj zapisy.
15 kwi 23:11
Eta:
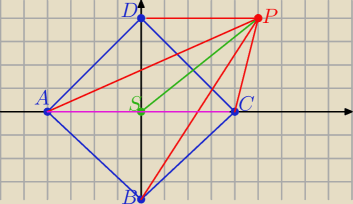
P(x,y) , S(0,0) A(a,0) , B(0,−a), C(a,0), D(0,a)
|PS|
2=x
2+y
2 i |AC|
2=4a
2
PC
2=(x−a)
2+y
2
PD
2=x
2+(y−a)
2
PB
2=x
2+(y+a)
2
PA
2=(x+a)
2+y
2
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
..... = 2x
2+2y
2+2x
2+2y
2 +4a
2 = 4(x
2+y
2)+4a
2= 4|PS|
2+|AC|
2
co kończy dowód
15 kwi 23:20
Eta:
Oooo już Mila mnie wyprzedziła
15 kwi 23:21
Eta:
Poprawiam chochlika : A(−a,0)
15 kwi 23:22
Saizou :
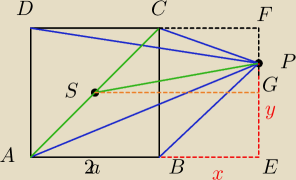
I porachować Pitagorasem

15 kwi 23:33
Szew: Dzięki

16 kwi 14:39
 P=(x,y), S=(a,a)
A=(0,0), B=(2a,0), C=(2a,2a), D=(0,2a)
1) |AC|=2a√2, |AC|2=8a2,
|PS|2=(a−x)2+(a−y)2=a2−2ax+x2+a2−2ay+y2=x2+y2+2a2−2a(x+y)
2)
|AP|2=x2+y2
|BP|2=(x−2a)2+y2
|CP|2=(x−2a)2+(y−2a)2
|DP|2=x2+(y−2a)2
3)
Suma kwadratów odległości od wierzchołków
Sk=2x2+2(x−2a)2+2*(y−2a)2+y2=
=4x2+4y2+12a2−8a*(x+y)
4) S=4|PS|2+|AC|2=4*[x2+y2+2a2−2a(x+y)]+8a2=
=4x2+4y2+8a2−8a(x+y)+8a2=
=4x2+4y2+12a2−8a(x+y)⇔
Sk=S
cnw
Posprawdzaj zapisy.
P=(x,y), S=(a,a)
A=(0,0), B=(2a,0), C=(2a,2a), D=(0,2a)
1) |AC|=2a√2, |AC|2=8a2,
|PS|2=(a−x)2+(a−y)2=a2−2ax+x2+a2−2ay+y2=x2+y2+2a2−2a(x+y)
2)
|AP|2=x2+y2
|BP|2=(x−2a)2+y2
|CP|2=(x−2a)2+(y−2a)2
|DP|2=x2+(y−2a)2
3)
Suma kwadratów odległości od wierzchołków
Sk=2x2+2(x−2a)2+2*(y−2a)2+y2=
=4x2+4y2+12a2−8a*(x+y)
4) S=4|PS|2+|AC|2=4*[x2+y2+2a2−2a(x+y)]+8a2=
=4x2+4y2+8a2−8a(x+y)+8a2=
=4x2+4y2+12a2−8a(x+y)⇔
Sk=S
cnw
Posprawdzaj zapisy.
 P(x,y) , S(0,0) A(a,0) , B(0,−a), C(a,0), D(0,a)
|PS|2=x2+y2 i |AC|2=4a2
PC2=(x−a)2+y2
PD2=x2+(y−a)2
PB2=x2+(y+a)2
PA2=(x+a)2+y2
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
..... = 2x2+2y2+2x2+2y2 +4a2 = 4(x2+y2)+4a2= 4|PS|2+|AC|2
co kończy dowód
P(x,y) , S(0,0) A(a,0) , B(0,−a), C(a,0), D(0,a)
|PS|2=x2+y2 i |AC|2=4a2
PC2=(x−a)2+y2
PD2=x2+(y−a)2
PB2=x2+(y+a)2
PA2=(x+a)2+y2
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
..... = 2x2+2y2+2x2+2y2 +4a2 = 4(x2+y2)+4a2= 4|PS|2+|AC|2
co kończy dowód
 I porachować Pitagorasem
I porachować Pitagorasem 
