matematykaszkolna.pl
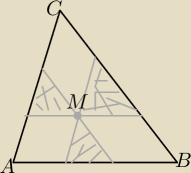
pole matmix: rysunek Pola zakreskowane są równe 8,18,32 Mam obliczyć pole trójkata ABC jak?
15 kwi 14:09
Eta: P(ABC)=(√P1+√P2+√P3)2 , P1,P2, P3 −− pola zakreskowane ................... P=162 ========
15 kwi 14:14
matt: A to skad ? ? ?
15 kwi 21:24
Eta: Wykaż ..... to się dowiesz skąd ? emotka
15 kwi 23:25
Eta: Może maturzyści wykażą ! Powodzenia emotka
16 kwi 22:42
Szkolniak: Rozumiem że odcinki w środku są równoległe do boków?
16 kwi 22:46
Eta: Tak
16 kwi 22:48
Eta: I jak idzie Szkolniak ?
16 kwi 23:13
Szkolniak: Miesza mi się wszystko nie wiem jakie równości wziąć by to wyszło − jedyne wiem że w gre wchodzą skale podobieństwa danych 3 trójkątów W szkole kiedyś robiłem podobne zadanie − z trapezem − i próbuje analogicznie zrobić, ale nie idzie
16 kwi 23:16
Eta: Dobrze myślisz emotka Dam Ci jeszcze czas ........
16 kwi 23:21
Mila: Szkolniak, to skończ zadanie 399988 Jest łatwiejsze, a może się kiedyś przydać.
16 kwi 23:21
Eta: Mila Niech Szkolniak pomyśli najpierw nad moim zadaniem emotka
16 kwi 23:28
Szkolniak: Eta jestem w stanie wyrazić wysokość dużego trójkąta za pomocą wysokości trzech mniejszych?
16 kwi 23:46
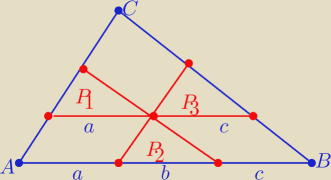
Eta: rysunek Z podobieństwa trójkątów T1, T2, T3 do ΔABC w skalach:
 a b c 
k1=
, k2=
, k3=
 a+b+c a+b+c a+b+c 
zatem (*) k1+k2+k3=1
 P1 
i
=k12 ...................
 P 
 √P1 √P2 √P3 
to k1=
, k2=
, k3=
 √P √P √P 
to z (*) ......................... P=(√P1+√P2+√P3)2 =================
16 kwi 23:48
Szkolniak: Czapki z głów emotkaemotka Czytając takie zadanie będąc na Twoim poziomie od razu widzi się rozwiązanie i wiadomo za co się wziąć czy też trzeba pokombinować? Bo czasami naprawdę ciężko z tą geometrią − człowiek próbuje na wszystkie sposoby i
16 kwi 23:52
Eta: Rozwiązuj zadania w świątek, piątek i niedzielę Trening czyni mistrza emotka
16 kwi 23:54
Szkolniak: Aj tam − byle na 30% z podstawowej emotka
16 kwi 23:56
Eta: Coooooooooooooo ?
16 kwi 23:57
Mila: Szkolniak, matmix, czy próbwaliście obliczyć pole bez wzoru podanego przez Etę ? To nie jest trudne.
17 kwi 17:06