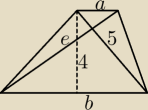
Pole trapezu Elena: Znaleźć pole trapezu wiedząc, że jego przekątne są do siebie prostopadłe, jedna z nich ma długość 5, a wysokość trapezu wynosi 4. Nie mam pomysłu jak obliczyć to pole, skorzystałam tylko z faktu, że suma kwadratów długości tych przekątnych jest równa kwadratowi sumy długości jego podstaw: e² + 25 = (a+b)² Jakaś dalsza wskazówka?

f123: hmm, moze dluzsze ramie uzaleznic od b − i pozniej z pitagorasa obliczyc b, mamy trojkat 3, 4,

	3		3
5 gdzie cosα =		i tw cosinusow: x2 = b2 + 52 − 10b *
	5		5

i pitagoras (b − 3)² + 4² = x². Narazie to mi tylko do glowy przychodzi, za 30 min bede przy komputerze to moge rozpisac (o ile to jest dobry pomysl)

f123: Dobra nie wazne, nie czytaj tego co napisalem

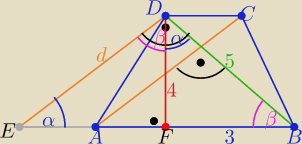
Eta: Z podobieństwa trójkątów BDF i EDF z cechy (kk)

5		3		20
	=		⇒ d=
d		4		3

	1
to P(trapezu)= P(ΔDEB) =		d*5=..
	2

	50
P=
	3

=========

Elena: Dziękuje, jednak nie rozumiem skąd równość P trapezu ABCD = P trójkąta DEB ?

Eta: Jeżeli przekątne trapezu są prostopadłe to

	1		1
P(trapezu)=		d1*d2 i P(ΔDEB)=		d1*d2
	2		2

wniosek .........

wredulus_pospolitus:

Eta: Co to za bohomaz ?

wredulus_pospolitus: Ciiii ... łatwiej tutaj rysować przestrzenne niż na tablicy on−line

Saizou : wredulus GeoGebra i screen i nie zaśmiecasz forum.

wredulus_pospolitus: Jakoś nigdy nie opanowałem GeoGebry

Saizou : To zwykły Paint