długość Nika: Długości boków trójkąta ABC są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę 120 stopni.Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta ABC jest równa 840. Oblicz objętość największej kuli jaka moze być umieszczona wewnątrz tego prostopadłościanu.

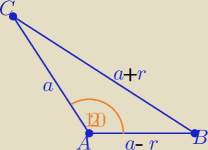
Eta: Z tw, cosinusów

	1
(a+r)2=a2+(a−r)2+2a*(a−r)*		bo cos120o= −1/2
	2

........................ 2a²−5r=0 ⇒ r=2a/5 to trójkąt ma wymiary

	3		7
a,		a,		a
	5		5

	21a3
V=840 ⇒		=840 ⇒ a3=1000 ⇒ a=10
	25

to prostopadłościan ma wymiary : 6,10,14 zatem największa kula w nim umieszczona musi mieć średnicę 2R=6

	4
Vk=		πR3=.......
	3

V_k=36π ========

Nika: dziękuję 🥰

Nika: tylko tam r chyba powinno być 1a/5

Nika: a nie sorki faktycznie r=2a/5

Eta: Widzę jeszcze chochlika : ............................. 2a²−5ar=0 ⇒ 2a−5r=0