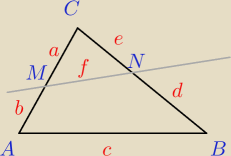
Trójkąt Szkolniak: Trójkąt ABC przecięto prostą MN tak, że punkt M należy do AC, a punkt N należy do BC. Powstałe wielokąty maja takie same pola i obwody. Udowodnij, że MN zawiera środek okręgu wpisanego w trójkąt ABC. 1) a+e+f=f+b+c+d ⇒ a+e=b+c+d 2) P_ΔMNC=P_ΔABC−P_ΔMNC ⇒ 2P_ΔMNC=P_ΔABC + wzór Herona (który mnie w tej sytuacji nie przekonuje) Jakaś wskazówka? Czy w ogóle powinienem to udowodnić z jakiejś równości?

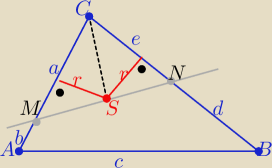Eta: Z treści zadania a+e=b+c+d ⇒ a+e =p −−− połowa obwodu ΔABC oraz z treści zadania

	1
P(CNM)=P(ABNM) ⇒ (*) P(CNM)=		P(ABC)
	2

Jeżeli S jest szukanym punktem wtedy:

	r		r		1
P(CNM)=P(CSM)+P(CNS)=		(a+e) =		*p=		P(ABC) −− zgodność z (*)
	2		2		2

co kończy dowód

Szkolniak: Dziękuję Eta

Eta: Na zdrowie