pochodne,parametr
bizi:

Funkcja f(x)=(m
2+1)x
3−4mx
2+5x−1 jest rosnąca w zbiorze liczb rzeczywistych dla:
a)m∊R
b)m∊(−
√15;
√15)
c)m∊<−
√15;
√15>
d)m∊(−
∞;−
√15)U(
√15;+
∞)
w odpowiedzi wychodzi c , lecz mi d
obliczenia:
f '(x)=3(m
2+1)x
2−8mx+5
Δ=(−8m)
2−4[3(m
2+1)]*5=64m
2−20(3m
2+3)=64m
2−60m
2−60
Δ=0 ==> 64m
2−60m
2−60=0 ==> 4m
2−60=0 ==> 4(m
2−15)=0 ==>4(m−
√15)(m+
√15)
m=−
√15 v m=
√15
f rośnie dla m∊(−
∞;−
√15),(
√15;+
∞)
gdzie zrobiłem błąd?
pozdrawiam i czekam na odpowiedz
14 kwi 18:47
bizi:
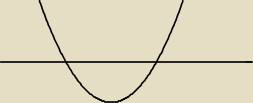
14 kwi 18:48
wredulus_pospolitus:
A przepraszam bardzo ... a co policzyłeś/−aś w miejscu:
Δ=0 ==> 4(m2−15)=0 ==>4(m−√15)(m+√15)
i jak to się ma do wniosku:
f rośnie dla m∊(−∞;−√15),(√15;+∞)
nawet jeśli to i ta by było wtedy:
m∊(−∞;−√15> u <√15;+∞)
14 kwi 19:00
bizi: No jak pochodna jest dodatnia w tym miejscu to funkcja f(x) rosnie tak?
14 kwi 19:09
wredulus_pospolitus:
dlatego warto używać JEDNOZNACZNYCH oznaczeń.
f'(x) = 3(m
2+1)x
2 − 8mx+5
Δ
x = 64m
2−60m
2−60
Δ
m = 4m
2 − 60

Ale zanim to .... to pytanie ważniejsze:
Aby funkcja f(x) była funkcją rosnącą w R, to co w takim razie się ma dziać z f'(x)

A kiedy to (odpowiedź na poprzednie pytanie) będzie zachodziło dla f'(x) tejże właśnie postaci

I jaki ma to związek z Δ
m 
14 kwi 19:12
f123: a gdzie zgubiles "−8mx" w liczeniu pierwszej delty?
14 kwi 19:13
wredulus_pospolitus:
fil ... nie zgubił/−a ... na początku jest (−8m)2 ... jest dobrze ... zły wniosek
wyciągnięty z wyznaczonej Δm
co wynika z ... nie przemyślenia sprawy nim się 'automatycznie' zaczęło rozwiązywać.
14 kwi 19:14
wredulus_pospolitus:
dobra ... ja się pośpieszyłem ... żadnego Δm nie ma ... on/−a po prostu nie wie " jakie
chce aby było f'(x) "
14 kwi 19:16
 Funkcja f(x)=(m2+1)x3−4mx2+5x−1 jest rosnąca w zbiorze liczb rzeczywistych dla:
a)m∊R
b)m∊(−√15;√15)
c)m∊<−√15;√15>
d)m∊(−∞;−√15)U(√15;+∞)
w odpowiedzi wychodzi c , lecz mi d
obliczenia:
f '(x)=3(m2+1)x2−8mx+5
Δ=(−8m)2−4[3(m2+1)]*5=64m2−20(3m2+3)=64m2−60m2−60
Δ=0 ==> 64m2−60m2−60=0 ==> 4m2−60=0 ==> 4(m2−15)=0 ==>4(m−√15)(m+√15)
m=−√15 v m=√15
f rośnie dla m∊(−∞;−√15),(√15;+∞)
gdzie zrobiłem błąd?
pozdrawiam i czekam na odpowiedz
Funkcja f(x)=(m2+1)x3−4mx2+5x−1 jest rosnąca w zbiorze liczb rzeczywistych dla:
a)m∊R
b)m∊(−√15;√15)
c)m∊<−√15;√15>
d)m∊(−∞;−√15)U(√15;+∞)
w odpowiedzi wychodzi c , lecz mi d
obliczenia:
f '(x)=3(m2+1)x2−8mx+5
Δ=(−8m)2−4[3(m2+1)]*5=64m2−20(3m2+3)=64m2−60m2−60
Δ=0 ==> 64m2−60m2−60=0 ==> 4m2−60=0 ==> 4(m2−15)=0 ==>4(m−√15)(m+√15)
m=−√15 v m=√15
f rośnie dla m∊(−∞;−√15),(√15;+∞)
gdzie zrobiłem błąd?
pozdrawiam i czekam na odpowiedz

 Ale zanim to .... to pytanie ważniejsze:
Aby funkcja f(x) była funkcją rosnącą w R, to co w takim razie się ma dziać z f'(x)
Ale zanim to .... to pytanie ważniejsze:
Aby funkcja f(x) była funkcją rosnącą w R, to co w takim razie się ma dziać z f'(x)  A kiedy to (odpowiedź na poprzednie pytanie) będzie zachodziło dla f'(x) tejże właśnie postaci
A kiedy to (odpowiedź na poprzednie pytanie) będzie zachodziło dla f'(x) tejże właśnie postaci
 I jaki ma to związek z Δm
I jaki ma to związek z Δm 