. Kappa: Siemanko, mam takie zadanie na logiczne myślenie, ale rysunek jest taki, że go tu nie dam rady w żaden sposób oddać. Chciałby ktoś pomóc poza forum?

wredulus_pospolitus: na dysk wirtualny wrzucasz i dajesz linka

wredulus_pospolitus: na jakim poziomie nauczania jesteś ?

Kappa: 1 rok studiów

Kappa: Wrzucę jak wrócę do domu

Kappa:

Kappa: https://drive.google.com/open?id=1wZKPB7aUEmYq1LEvHwmDt1AwaJhJH7Q5 https://drive.google.com/open?id=1k5yxM9s4Wx-9kJIYVVOQhMLeCWtxp6M0

Kappa: Zad 16, 20 i 21

Kappa: Help pls

Saizou : Tip: przygotuj takie kostki i sam poukładaj te budowle

Saizou : Swoją drogą wygląda jak dydaktyka matematyki jakaś.

aniabb: w 16. 18 klocków w 20. PFFPF w 21. 12 klocków

wredulus_pospolitus: 16. co najwyżej (osobno na każdym poziomie): 9 + 9 + 1 = 19 co najmniej (osobno na każdym poziomie) 5 + 5 + 1 = 11 rysunek przedstawia 'widok z góry' (na czerwono pokazana 'warstwa więcej' )

wredulus_pospolitus: Powyższe zadanie może być pomocne do 'załapania' kreski dla przyszłych studentów budownictwa / 'szambonurkologii' i innych kierunków wymagających od absolwentów pracy z projektami (m.in. budowlanymi)

aniabb: myślałam 19 a napisałam 18 ..wrr...

wredulus_pospolitus: 20. zauważ, że mamy zależność: numer poziomu = n liczba dużych półkoli = 2n−1 liczba małych części kół = 2*(2n−1) liczba odcinków prostych = 2n (ponieważ mamy dokładnie (2n−2) odcinków łączących sąsiadujące elementy (których jest 2n−1 ... więc połączeń będzie o jeden mniej) + 2 'krótsze' odcinki proste ... po jednym dla pierwszego i ostatniego elementu danego poziomu stąd: a) 9 ; 18 ; 10 więc P b) 143 ; 286 ; 144 więc F c) .... d) ... e) ...

aniabb: a w 21 nie ma założenia że muszą stać na innym i też pewnie da się zrobić z 10

aniabb: liczba odcinków prostych to jest 2xilość elementów I rodzaju, których jest tyle ile nr poziomu czyli 2n a tych drugiego rodzaju jest na każdym poziomie n−1

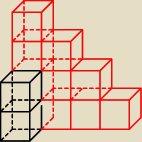
wredulus_pospolitus: 21. (liczymy rzędy od lewej − patrząc na klocek od przodu) liczba klocków to: (2+4) + 3 + 2 + 1 = 12 rysunek imituje wizualizację 3d

wredulus_pospolitus: aniabb −−− jeżeli nie muszą stać jeden na drugim, to może być 10, 11 lub 12

wredulus_pospolitus: nieskromnie przyznam, że nawet nieźle wygląda ten rysunek klocków (myślałem że będzie to gorzej wyglądało)

wredulus_pospolitus: I tak jak napisałem wcześniej −−− zadanie 'jak znalazł' jako wstęp do kreski dla studentów −−− czyli budowanie wyobraźni przestrzennej na podstawie płaskich rzutów

aniabb: ano bardzo ładnie ... podziwiam za cierpliwość i precyzję ... mi tutejsze figury się mocno rozjeżdżają

wredulus_pospolitus: teraz jak patrzę na to ... to widzę że paru linii przerywanych pod koniec nie zrobiłem

aniabb: zad 17 17 samochodów 2 P 9 K 4

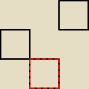
wredulus_pospolitus: ad 16. poprawka do najmniejszej liczby możliwych kostek, będzie to: 3 + 3 + 1 = 7 ponieważ nie mamy informacji, że klocki musza się stykać z bokami (przykładowy rzut z góry)

aniabb: teraz zauważyłam że chcą co najmniej i co najwyżej

Kappa: Wielkie dzięki, naprawdę szacun.

wredulus_pospolitus: Kappa −−− na jakim kierunku jesteś Będziesz mieć 'kreskę' na studiach

Kappa: Architektura

wredulus_pospolitus: No to kreska jak nic Ciebie czeka (a może to nawet z kreski jest zadanie). Tak więc −−− musisz ćwiczyć 'wyobraźnie 3D', aby szybko i sprawnie móc operować na rzutach.

wredulus_pospolitus: Mam nadzieję, że rozwiązania (i rysunki) są pomocne i rozumiesz 'co i jak' się dzieje w tych konkretnych zadaniach.