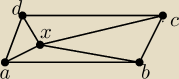
Równoległobok xoxo: Punkt X leży wewnątrz równoległoboku ABCD. Pokaż, że P_ABX + P_CDX = P_BCX + P_ADX. Jakaś podpowiedź, wskazówka od czego zacząć, ponieważ nie mam pomysłu

ford: przez punkt x poprowadź dwie proste jedną równoległą do AD drugą równoległą do AB

xoxo: Tak zrobiłam, ale nie widzę co dalej można z tym zrobić..

wredulus_pospolitus: Skorzystaj z 'faktu oczywistego': Pole równoległoboku = |AB|*h_pionowa = |AD|*h_pozioma I zauważ, że h_ΔABX + h_ΔCDX = h_pionowa analogicznie z drugą parą trójkątów

f123:

ah1		ah2		bh3		bh4
	+		+		+		= a(h1 + h2)
2		2		2		2

bh3		bh4		ah1		ah2
	+		=		+
2		2		2		2

====

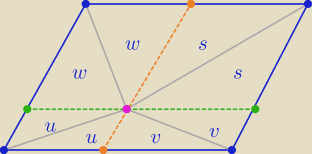
Eta: I po ptokach