Udowodnić, że AB jest prostopadła do PQ
Elena:
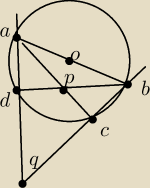
Punkty C i D leżą na okręgu o średnicy AB. Proste AC i BD przecinają się w punkcie P, proste AD
i BC
przecinają się w punkcie Q. Pokaż, że prosta AB jest prostopadła do PQ.
Zauważam, że w trójkącie APB: BC i AD są jego wysokościami oraz kąt ACQ=90 stopni i kąt
BDQ=90 stopni.
Jednak dalej nie wiem jak poprowadzić te dowód i czy ta informacja jest tu przydatna

14 kwi 14:19
klop: zauwac, ze na czworokacie dqcp mozna opisac okrag
14 kwi 14:30
Elena: Ok więc na czworokącie DPCQ można opisać okrąg o średnicy PQ, tylko nie wiem jak dowieść, że
ta średnica jest prostopadła do AB..
14 kwi 16:11
Saizou :
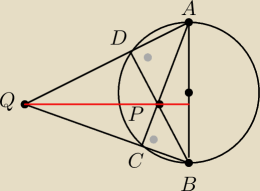
Może tak
BD jest wysokością trójkąta BQA (BDA oparty na średnicy AB)
AC jest wysokością trójkąta BQA (ACB oparty na średnicy AB)
Wysokości te przecinają się w punkcie P
Prowadzimy wysokość z wierzchołka Q na bok AB.
Przecina ona punkt P (wysokości przecinają się w jednym punkcie), zatem
QP jest prostopadła do AB
14 kwi 17:10
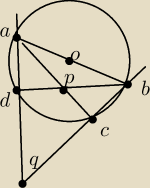 Punkty C i D leżą na okręgu o średnicy AB. Proste AC i BD przecinają się w punkcie P, proste AD
i BC
przecinają się w punkcie Q. Pokaż, że prosta AB jest prostopadła do PQ.
Zauważam, że w trójkącie APB: BC i AD są jego wysokościami oraz kąt ACQ=90 stopni i kąt
BDQ=90 stopni.
Jednak dalej nie wiem jak poprowadzić te dowód i czy ta informacja jest tu przydatna
Punkty C i D leżą na okręgu o średnicy AB. Proste AC i BD przecinają się w punkcie P, proste AD
i BC
przecinają się w punkcie Q. Pokaż, że prosta AB jest prostopadła do PQ.
Zauważam, że w trójkącie APB: BC i AD są jego wysokościami oraz kąt ACQ=90 stopni i kąt
BDQ=90 stopni.
Jednak dalej nie wiem jak poprowadzić te dowód i czy ta informacja jest tu przydatna 
 Może tak
BD jest wysokością trójkąta BQA (BDA oparty na średnicy AB)
AC jest wysokością trójkąta BQA (ACB oparty na średnicy AB)
Wysokości te przecinają się w punkcie P
Prowadzimy wysokość z wierzchołka Q na bok AB.
Przecina ona punkt P (wysokości przecinają się w jednym punkcie), zatem
QP jest prostopadła do AB
Może tak
BD jest wysokością trójkąta BQA (BDA oparty na średnicy AB)
AC jest wysokością trójkąta BQA (ACB oparty na średnicy AB)
Wysokości te przecinają się w punkcie P
Prowadzimy wysokość z wierzchołka Q na bok AB.
Przecina ona punkt P (wysokości przecinają się w jednym punkcie), zatem
QP jest prostopadła do AB