Algorytm Olek: Najszybszy algorytm znalezienia dwóch pozostałych wierzchołków kwadratu. Dostajemy dwa wierzchołki kwadratu i musimy znaleźć dwa pozostałe, zależy mi na jak najszybszym algorytmie znalezienia pozostałych wierzchołków. Mi do głowy przyszły dwa, ale są zbyt trudne do napisania mianowicie jeden z nich to najbardziej popularny sposób czyli 1)długość AB 2)współczynnik kierunkowy AB 3)dwie proste prostopadłe do AB, jedna przechodzi przez A druga przez B 4) do wzoru na długość odcinka wstawiamy dane punktu który otrzymaliśmy a za y punktu który szukamy wstawiamy wzór prostej która przez niego przechodzi znajdujemy x_c potem y_c i tak samo robimy dla punktu D. Ale niestety algorytm musi być zrozumiały dla komputera dla komputera, ten oczywiście można użyć ale przy liczbach wymiernych jest z tym dużo problemu. Wiem, że to nie jest forum informatyczne, ale po prostu może ktoś zna jakiś szybki sposób na znalezienie tych wierzchołków. Coś żeby nie było dużej ilości wzorów.

Olek: O może ktoś wie jak zrobić takie zadanie maturalne na wektorach?

wredulus_pospolitus: Zacznijmy od tego −−− te dwa znane wierzchołki to kolejne wierzchołki czy dowolne (czyt. możliwe że połączone są przekątną kwadratu)

Olek: dwa kolejne

f123: Ale na wejsciu dostajemy dwa dowolne wierzcholki kwadratu?

wredulus_pospolitus: czy te dwa konkretne są też w konkretnej kolejności: czyli A −> B czy może być B − > A I czy taki kwadrat wchodzi w grę? Czy przyjmujemy że opis wierzchołków jest przeciwny do ruchu wskazówek zegara

wredulus_pospolitus: w jakiej przestrzeni jesteśmy (ile współrzędnych mają punkty)

f123: @wredulus jak mozesz, chodzi na discorda mam pare pytan

Olek: Tak brzmi polecenie: program prosi i podanie dwóch punktów na płaszczyźnie, odczytuje punkty wprowadzone przez użytkownika, a następnie wypisuje współrzędne dwóch punktów, które wraz z podanymi tworzą wierzchołki kwadratu (uwaga zadanie geometryczne ma dwa rozwiązania − program powinien wypisać obie możliwości

wredulus_pospolitus: No to w takim razie: 1) Nie ma informacji że są to DWA KOLEJNE wierzchołki 2) Zachowany jest opis przeciwny z ruchami wskazówek zegara

wredulus_pospolitus: Najszybciej −−− na wektorach

Olek: A tak mniej więcej jak zrobić to na wektorach? Bo właśnie w szkole średniej jedynie dodawaliśmy wektory, mnożyliśmy przez liczbę, liczyliśmy długość ale jakoś nigdy żadnego większego zadania z nimi nie robiliśmy

jc: Jedno z 4 rozwiązań: A=(p,q), B=(r,s) C=(r+q−s, s+r−p) D=(p+q−s, q+r−p)

Olek: jc z czego to wynika?

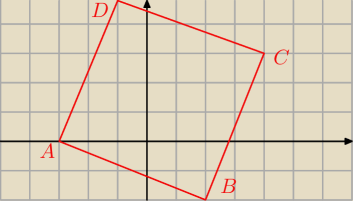
wredulus_pospolitus: narysuj sobie kwadrat i zobacz 'o ile zmieniają' się współrzędne przy 'przejściu z A do B' o ile zmieniają się gdy idziesz z B do C zauważ zależność ... sprawdź czy będzie działać to przy przejściu z C do D (ewentualnie zrób analogicznie −−− przejście z B do A i jak wtedy będzie wyglądało przejście z A do D)

Olek: Próbuję cały czas rozgryźć ten sposób i mi nie idzie

Olek: Drugie rozwiązanie to: C(r−q +s, s−r + p) D(p − q +s, q − r + p) tak?