parametry salamandra: Dane jest równanie (k−2)x²−(k+1)x−k=0 o niewiadomej x. Wyznacz zbiór wartości parametru k, dla których to równanie ma: a) tylko ujemne rozwiązania b) rozwiązania x1 i x2 spełniające warunek |x1|+|x2|≤1 https://imgur.com/a/LOo55Ev mógłby ktoś zerknąć? łatwo w takim zadaniu o prosty błąd, a odpowiedzi niestety nie posiadam

wredulus_pospolitus: pytanie: dlaczego zakładasz, że Δ > 0

salamandra: Pytałem na discordzie o to, ale nikt nie odpowiedział, to zaryzykowałem, że >0

Saizou : @wredulus, przypadek liniowy jest później rozwiązany

salamandra: Poza tym jak sprawdzę a=0 to chyba sprawdzam jedno rozwiazanie? Czy podwójne tez muszę sprawdzić czyli Δ≥0

Saizou : Δ ≥ 0, może być miejsce zerowe podwójne.

Jerzy: 20:43 , słuszna uwaga.Przecież może być jedno rozwiązanie ujemne.

salamandra: Mówisz o podwójnym rozwiązaniu Jerzy? I o podpunkcie a)?

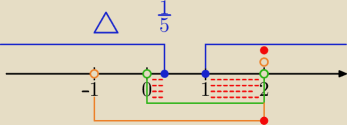
Mila: równanie: (k−2)x²−(k+1)x−k=0 a) 1) k=2 to otrzymujemy równanie : −3x−2=0

	2
x=/div>		<0
	3

lub 2) k≠2 Δ=(k+1)²+4*k*(k−2)=k²+2k+1+4k²−8k=5k²−6k+1

	1
2.1) Δ≥0⇔k≤		lub k≥1
	5

i 2.2) x₁*x₂>0 ⋀x₁+x₂<0

	−k		k+1
x1*x2=		>0⇔k∊(0,2) i		<0⇔(k+1)*(k−2)<0⇔k∊(−1,2)⇔x∊(0,2)
	k−2		k−2

3) (1 ⋁2) suma warunków

	1
x∊(0,		>∪<1,2>
	5

Czerwoną kropkę dodałam dla k=2 z (1) warunku. Za chwilę (b)

salamandra: Dziękuję Milu, w sumie warunków chyba powinno być (1;2), a nie <1;2>, bo z x1+x2 mamy (1;2)?

salamandra: nie było pytania już jasne

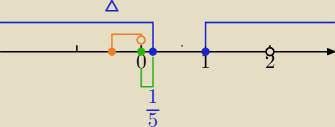
Mila: b)k≠2

	1
1) (*) Δ≥0⇔k≤		lub k>2
	5

|x₁|+|x₂|≤1 /²⇔ (x₁+x₂)²−2x₁*x₂+2|x₁*x₂|≤1⇔

	k+1		2k		−k
(		)2+		+2*|		|≤1 i (*)
	k−2		k−2		k−2

	−k		−k
2) |		|=		dla (−k)*(k−2)≥0⇔k∊<0,2) i (*)⇔
	k−2		k−2

	1
(**) k∊<0,		>∪<1,2)
	5

	k+1		2k		−k
Wtedy mamy nierówność:(		)2+		+2*		≤1 ⇔
	k−2		k−2		k−2

	k+1
(		)2≤1
	k−2

(k+1)²≤(k−2)²⇔

	1
k≤		i (**)⇔
	2

	1
(***) k∊<0,		>
	5

============ lub

	−k		k
3)|		|=		dla k< 0 lub k>2 i Δ≥0
	k−2		k−2

Wtedy mamy nierówność:

	k+1		2k		k
(		)2+		+2*		≤1
	k−2		k−2		k−2

	k+1		4k
(		)2+		≤1⇔
	k−2		k−2

U{(k+1)²+4k*(k−2)}{(k−2)²≤1 /*(k−2)² k²+2k+1+4k²−8k≤k²−4k+4⇔ 4k²−2k−3≤0 Δ=52

1−√13		1+√13
	≤k≤		i k< 0 lub k>2 i Δ≥0⇔
4		4

1−√13
	≈−0.65
4

	1−√13
(****)k∊(		,0)
	4

=============== 4) Suma (**),(****)

	1−√13		1
k∊<		,		>
	4		5

==================

salamandra: Dzięki