stereometria anonim123: Dany jest trójkąt prostokątny. Niech V1 i V2 oznaczają objętości brył powstałych w wyniku obrotu tego trójkąta kolejno wokół obu przyprostokątnych, a V3 − wokół

	1		1		1
przeciwprostokątnej. Wykaż, że		+		=		.
	V12		V22		V32

Saizou :

	1
V1=		πa2b
	3

	1
V2=		πb2a
	3

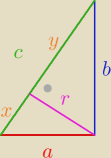
	1		1		1
V3=		πr2x+		πr2y=		πr2c
	3		3		3

c=√a²+b² i teraz rachunki

anonim123: Nie potrafię sobie wyobrazić dlaczego V₃ jest równe tyle co napisałeś

anonim123: Mogę prosić o rysunek tylko przypadku opatrzonego zapisem V₃

Eta:

	ab
h1+h2=c r3=
	c

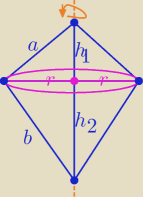
	1		1		1
V3 =		π r32h1+		πr32h2 =		πr32*(h1+h2)
	3		3		3

	1
V3=		πr32*c
	3

V₃=πa²b²/3c

anonim123:

	ab
Skąd w rozwiązaniu r3=
	c

Eta:

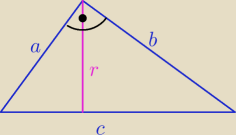
	ab		c*r		ab
PΔ=		i PΔ=		⇒ r=
	2		2		c

anonim123: A w ostatniej linijce wyrażenie jest pomnożone przez 3c?

Eta: Podzielone przez 3c

Eta:

	1		a2b2
V3=		πr32c r32=
	3		c2

	πa2b2
to V3=
	3c

anonim123: Dziękuję