trudne maturka: Dany jest trójkąt równoboczny ABC Oblicz pole trójkąta MNK otrzymanego przez zgięcie trójkąta ABC względem prostej MN tak,że wierzchołek C znalazł się w punkcie K na boku AB

	1
przy czym |BK|=		|AB|,zaś punkt M∊AC i punkt N∊BC
	3

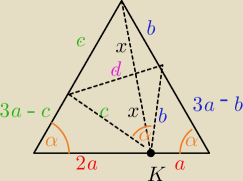wredulus_pospolitus: α = 60^o wyznacz 'c' zależne od 'a' ; 'b' zależne od 'a'.

	b*c*sinα
Oblicz pole trójkąta MNK ze wzoru: P =
	2

a7:

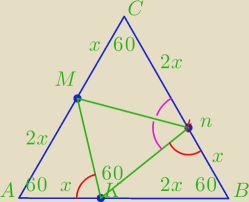
	9√3
PΔABC=1/2*3x*3x*sin60=		x2
	4

trójkąty CMN i KMN są przystające , trójkąty AMK i KNB okazują się być podobne i potem wynika z tego, że wszystkie są podobne

	√3
PΔAMK=1/2x*2x*sin60=		x2
	2

	3√3
PΔMNK=PΔABC−3*PΔAMK=		x2
	4

a7:

	3√3		a2		a2√3
jeśli mamy dany bok a to x=1/3*a to PΔMNK=		*		=
	4		9		12

Mila: Dla |AB|=a

	49a2√3
PΔKMN=
	720

Eta: Mam taki sam wynik Ja liczyłam dla |AB|=6a

	49a2√3
P=
	20

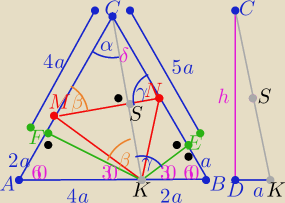Eta: |AB|=6a , h=3√3 |DK|=a to |CK|=2√7a , |CS|=a√7 i z trójkątów "ekierek" |FK|=2a√3 i |EK|=a√3 ...... pozostałe oznaczenia na rysunku z podobieństwa trójkątów: KFC i MSC oraz KEC i NSC z cechy (kk)

2a√3		4a		a√3		5a
	=		i		=
|MS|		a√7		||NS|		a√7

	a√21		a√21
to |MS|=		i |NS|=
	2		5

	7a√21
|MN|=
	10

	1		1		7a√21
P(KMN)=		*|MN|*|KS| =		*		*a√7
	2		2		10

	49a2√3
P(KMN)=
	20

=============