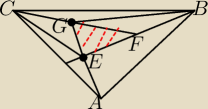
Zadanie Monia: Pole zamalowanego trójkąta jest równe 1. Oblicz pole trójkąta ABC, wiedząc, że |AE|=|EG|, |EF|=|FB|, |FG|=|GC|. Przedstaw swoje rozumowanie.

ite: |EF|=|FB| → P_EFG=P_BFG=1 (trójkąty mają wspólną wysokość) |AE|=|EG| → itd. |FG|=|GC| → wyszukaj trójkąty o równych podstawach i wysokościach

a7: PΔFBG=1 PΔCGB=1 (ta sama podsatwa co FGi ta sama wysokość) PΔAEB=2 PΔCGE=1 (podstawa CG=GF wspólna wysokość) PΔCEA=1 (GE=AE , wspólna wysokość, a wcześniej PΔCGE=1) PΔABC=1+1+1+2+1+1=7