mtura
f123: W dowolnym czworokacie f1 polaczono srodki kolejnych bokow otrzymujac czworokat F2. W
czworokacie F2 polaczono srodki kolejnych bokow otrzymujac czworokat F3 itd. Oblicz sume pol
nieskonczonej liczby tych czworokatow wiedzac, ze pole czworokata F1 jest rowne P
11 kwi 18:16
janek191:
PCZ = 2 P
11 kwi 18:21
f123: @jnake191 super, ale prosze o uzasadnienie

11 kwi 18:24
janek191:
Najpierw należy udowodnić,że pole kolejnego czworokąta jest równe połowie
pola wyjściowego czworokąta. Otrzymujemy nieskończony ciąg geometryczny tych pół
o ilorazie q = 12.
11 kwi 18:28
f123: @janek191 tez tak "zalozylem", ale nie wiem jak to udowodnic
11 kwi 18:29
janek191:
Ja to kiedyś udowodniłem i zapisałem rozwiązanie na zadane.pl
Trzeba odnaleźć to rozwiązanie. trzeba skorzystać z Tw. talesa.
Janek191
Teraz nie mam czasu .
11 kwi 18:34
janek191:
Talesa

11 kwi 18:34
f123: dd
11 kwi 20:07
wredulus_pospolitus:
janek −−− Tales nie załatwia sprawy, bo jest to dla DOWOLNEGO czworokąta wypukłego, więc boki
nie muszą być równoległe
11 kwi 20:07
ite:
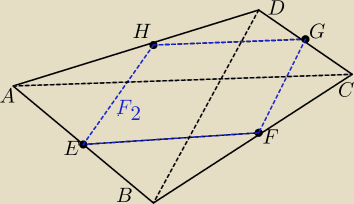 wredulus
wredulus w F
2 są równoległe
11 kwi 20:32


 wredulus w F2 są równoległe
wredulus w F2 są równoległe