matura f123:

	x3
Uzasadnij ze rownanie		− 2 = 0 ma dokladnie jedno rozwiazanie
	x + 1

wredulus_pospolitus: proponowana metoda: Krok 1) pochodna Krok 2) ekstrema + monotoniczność Krok 3) wartości w ekstremach Krok 4) granice na krańcach przedziałów + punkcie nieciągłości Krok 5) wnioski z kroków 2,3 i 4 odnośnie 'odpadających' przedziałów Krok 6) tw. Dirichleta + monotoniczność dla jedynego przedziału w którym może być rozwiązanie

f123: @wredulus_pospolitus to dawaj moze discorda, bo tak robie i jakos nie wychodzi

f123: w sumie juz sobie poradzilem

wredulus_pospolitus:

Saizou :

x3
	−2=0
x+1

	2
x3−2x−2=0 i podstawić x=y+
	3y

i otrzymamy

	8
y3+		−2=0 y3=t
	27y3

	8
t2−2t+		=0
	27

obliczyć pierwiastki i powracać z podstawieniem

ICSP: x³ − 2x − 2 = 0

	−2
Δ = (		)3 + 1 > 0 − równanie ma jeden pierwiastek dodatni
	3

ICSP: Co wy macie z tym wyznaczaniem pierwiastków ?

ICSP: 17:54 − bez słowa dodatni.

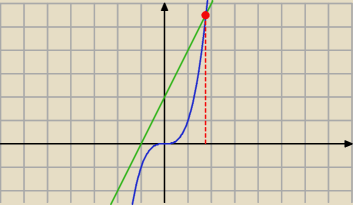
Eta: x≠ −1 x³=2x+2 y=x³ i y=2x+2