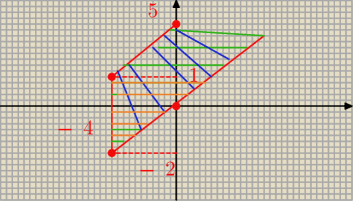
Układy nierówności Shizzer: Zbiór A (fragment zbioru A pokazano na rysunku) jest zbiorem punktów, których współrzędne spełniają pewien układ trzech nierówności liniowych z dwiema niewiadomymi. Znajdź taką wartość współczynnika b, aby prosta o równaniu y = −3x + b miała tylko jeden punkt wspólny ze zbiorem A. Odp: b = −14 Poprawny układ równań opisujący zbiór punktów A to:

⎧	x ≥ −4
⎨	y ≥ 12x
⎩	y ≤ x + 5

Próbowałem zrobić to w ten sposób:

⎧	y = −3x + b
⎜	2y ≥ 0
⎨	y ≥ x + 5
⎩	x ≥ −4

⎧	2(−3x + b) ≥ 0
⎨	−3x + b ≥ x + 5
⎩	x ≥ −4

⎧	−6x + 2b ≥ 0
⎨	b ≥ 4x + 5
⎩	x ≥ −4

⎧	b ≥ 3x
⎨	b ≥ 4x + 5
⎩	x ≥ −4

Następnie próbowałem zrobić to w sposób graficzny. Nie znalazłem pojedynczego punktu, który byłby w tym przypadku rozwiązaniem. Pomyślałem, że być może niedokładnie narysowałem proste więc sprawdziłem czy proste o równaniach y=3x, y=4x+5, x=−4 przecinają się w jednym punkcie, ale z układu równań wyszło mi, że taki punkt nie istnieje. Proszę więc o pomoc w rozwiązaniu tego zadania. Wyczerpały mi się pomysły

Shizzer: Znalazłem błąd w swoim układzie równań dlatego spróbuję na razie sam to zadanie rozwiązać. Jak będą problemy to dam znać

Shizzer: Końcowy układ równań powinien wyglądać tak (chyba):

⎧	x ≥ −4
⎨	b ≤ 72x
⎩	b ≤ 4x + 5

Wyobraziłem sobie, że żeby zbiór punktów ograniczających jakąś półpłaszczyznę miał dokładnie 1 rozwiązanie to proste ograniczające te półpłaszczyzny muszą się przeciąć (jeśli dobrze myślę). Więc pasowałoby rozwiązać taki układ równań:

⎧	x = −4
⎨	b = 72x
⎩	b = 4x + 5

Niestety powyższy układ równań nie ma rozwiązań i nie wiem jak to ruszyć dalej.

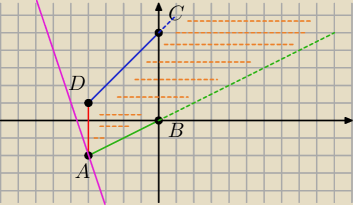
Saizou : prosta y=−3x+b jest malejąca, zatem jedynym punktem wspólnym tej prostej oraz obszaru może być punkt A=(−4,−2) −2=−3*(−4)+b b=−14

Shizzer: Dziękuję bardzo! Świetne rozwiązanie − sprytne Jeśli miałbym wyznaczyć jeden punkt wspólny zbioru punktów półpłaszczyzny ograniczonej prostymi to dobrze myślałem, że trzeba znaleźć punkt przecięcia się tych prostych granicznych? Bo tutaj jak widać można to zrobić dużo prościej i sprytniej, ale mając inny układ tej półpłaszczyzny chyba nie będzie to zawsze tak oczywiste?

Saizou : można i tak, ale byłoby o wiele więcej liczenia