matura Kamil18: 2. Macie jakieś fajne zadanie przygotowujące do matury rozszerzonej?

ite: Dla jakich wartości parametru m rówanie (−1+2*log_1/2 m)x² − 2x + log_1/2 m = 0 ma co najmniej jedno rozwiązanie?

Jerzy: Wskazówka: Nie zapomnieć o sprawdzeniu m = √0.5

Jerzy: A licząc wyróżnik, wygodnie podstawić: log_1/2m = t

Kamil18: Ok zrobiłem wyszło mi 1/2<m<√2 +√2/2.

Kamil18: Dobra odpowiedz?

ford: powinno wyjść 1/2 < m < √2

ford: Oczywiście znaki ≤ zamiast <

ite: Dodam zadanie z tak lubianymi kątami dwuściennymi (pkt a i b): Krawędź boczna ostrosłupa prawidłowego trójkątnego jest dwa razy dłuższa od krawędzi podstawy. Wyznacz cosinus kąta dwuściennego utworzonego przez: a/ parę ścian bocznych, b/ ścianę boczną i płaszczyznę podstawy, c/ krawędź boczną i wysokość przeciwległej ściany bocznej.

Mila: zadanie 1. Podstawą graniastosłupa prostego jest równoległobok. Przekątne graniastosłupa mają długości 9cm i √13 cm. Obwód podstawy równa się 18 cm, a krawędź boczna ma długość 4 cm. Oblicz objętość tego graniastosłupa.

Banach : Suma dlugosci wszystkich krawedzi prostopadloscianu o podstawie kwadratu wynosi 24 cm . Obliczyc powierzchnie calkowita prostopadloscianu o najwiekszej objetosci

Mila: Zadanie 2. Ostrosłup prawidłowy trójkątny o boku podstawy a jest wpisany w sferę, przy czym środek tej sfery dzieli wysokość ostrosłupa w stosunku √5:1 licząc od wierzchołka . Wyznacz objętość tego ostrosłupa.

Mila: Dzisiaj młodzież odpoczywa

f123: @Mila nie, robia kolejny arkusz

Mila: Powodzenia Dobranoc

Kamil18: Ite a) 7/15 Zad 1 64 cm³ Banach Pc=6*(8/3)³ Zad 2 V=a³*(√5+1)/24 Trochę zeszło ale było tego dużo, coc nie wiem czy dobrze

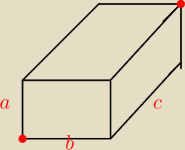
liceum: Zad 3 Ile wynosi najkrótsza droga między zaznaczonymi wierzchołkami po powierzchni prostopadłościanu jeśli a<b<c?

Kamil18: Czy to bedzie √b²+c²+a

ite: 17:54 a/ 7/15 więc dobra odpowiedź 👍🏼

Kamil18: ite b) √5/15

Kamil18: W tym zad 3 to dorze?

Banach: Banach do Kamil18 , niestety zly wynik , Szkic rozwiazania ! 8a + 4h = 24 ⇒ h= 6−2a V= a²h ⇒ V(a) = a²( 6 −2a) ⇒ V(a) = −2a³ +6a² V '( a) = −6a² + 12 a V' (a) = 0 ⇒a= 0 lub a= 2 , h = 2 V_max dla a= 2 P_c = 6a² = 24 cm²

Kamil18: Ok tak zuważyłem ten bład u mnie. A jak wykonać to zad 3

Banach: F(x) = √ b² + x² + √ c² + ( a − x )² x − odleglosc punktu P lezacego na pionowej krawedzi w odleglosci od dolnego wierzcholka Oblicz F '(x) = 0 , i.t.d ..........

Kamil18: "x − odleglosc punktu P lezacego na pionowej krawedzi w odleglosci od dolnego wierzcholka " co to znaczy?

Banach: Na pionowej krawedzi oznacz punkt P , x − odleglosc tego punktu od dolnego wierzcholka tej krawedzi .( patrz rysunek do zad.3) d₁ = √b² + x² , twierdzenie Pitagorasa dla Δ lezacego na przedniej scianie prostopadloscianu , drugie wyrazenie dla bocznej sciany .

Kamil18: Jakoś nie widzę tej drogi, możesz ją jakoś zaznaczyć na rysunku?

ite: 17:54 b/ cos β = √5/15 super, możesz zacząć święta

Kamil18: A to zad. 3 nie wiem jak?

ite: Banach to na pewno wytłumaczy, ja wyjaśnie tylko, że najkrótsza droga nie musi prowadzić (tak jak zapisałeś 10:23) po przekątnej ściany i wzdłuż którejkolwiek krawędzi. Może przecinać krawędź, właśnie w pkcie P.

Kamil18: Ok choć pewnie bez rysunku nie dam rady

Saizou : Kamil zrób rysunek siatki tego prostopadłościanu i zaznacz szukaną odległość

Kamil18: Taką klasyczną siatkę?

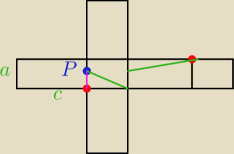
Kamil18: o chodzi o te "zielone" odcinki

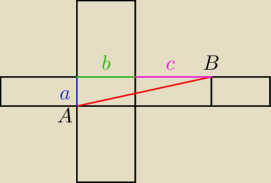
Saizou : |AB|=√a²+(b+c)²

Kamil18: Co ozancza ten odcinek AB

Kamil18: To jest ta odpowiedź

ite: AB − najkrótsza droga między wierzchołkami A i B

Kamil18: Takie proste to było bez pochodnych?

Saizou: Nie zawsze jest potrzebny skomplikowany aparat matematyczny