zadanie otwarte anonim123: Jak to rozwiązać? Punkty A,B,C,D,E,F są kolejnymi wierzchołkami sześciokąta foremnego,przy czym A = (0,0) i D = (4,0). Wyznacz równanie stycznej do okręgu opisanego na tym sześciokącie,przechodzącej przez punkt F leżący w 1 ćwiartce układu współrzędnych.

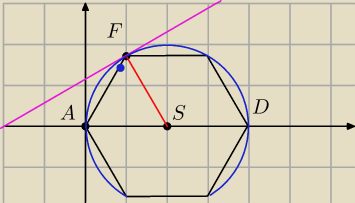
Saizou : F=(1,√3) S=(2,0)

	√3−0
ASF=		=−√3
	1−2

	√3
prosto prostopadła do SF ma współczynnik równy
	3

	√3
y=		+b
	3

przechodzi ona przez punkt F

	√3
√3=		+b
	3

	2√3
b=
	3

	√3		2√3
y=		x+
	3		3

anonim123: Skąd F=(1,√3)?

Jerzy: To wysokość trójkąta równobocznego o boku 2

anonim123: Dzięki

anonim123: A w ten sposób obliczyłam jedną współrzędną y a co z drugą?

anonim123: Już wiem

anonim123: A jeszcze mam pytanie co jest oznaczone za pomocą ASF

Jerzy: ASF to trójką, ale A_SF to obliczenie współczynnika kierunkowego prostej SF

anonim123: za pomocą jakiego wzoru został obliczony współczynnik kierunkowy?

Jerzy:

	yF − yS
F(1,√3) oraz S(2,0) k =		.
	xF − xs

Mozna też prościej. Prosta SF jest nachyloha do dodatniej osi OX pod katem 120^o , a tg120^o = − √3

anonim123: A nie pod kątem 60 stopni?

Jerzy: Współczynnik kerunkowy prostej, to kąt nachylenia tej prostej do dodatniej części osi OX

anonim123: A dlaczego pod katem 120 a nie 60?

anonim123: Już rozumiem

anonim123: Dziękuję za pomoc już wszystko jest zrozumiałe