trygonometria anonim123: Zadanie tutaj https://zapodaj.net/23f019cfd98ef.jpg.html wraz z rozwiązaniem czy to jest poprawne?

Jerzy: No niestety nie.

	π		π
W podanym przedziale cos jest rosnący, czyli: 3x >		⇔ x >
	3		9

anonim123: Nie rozumiem, dlaczego moje rozwiązanie nie jest prawidłowe

Jerzy: Moje też

	1		π		2kπ		π		2kπ
cos3x >		⇔ −		+		< x <		+		i teraz wybierz katy z
	2		9		3		9		3

	π
przedziału [0,		]
	2

anonim123: Nie rozumiem na jakiej zasadzie zostały wybrane kąty. Rozwiązanie z książki również jest dla mnie niezrozumiałe nie rozumiem treści punktowanej za 3 punkty rozwiązanie zadania https://zapodaj.net/b77e69c21d123.jpg.html i nadal nie wiem dlaczego moje rozwiązanie jest złe?

Jerzy:

	u		1
Dokonano podstawienia: 3x = u ⇔ x =		. Rozwiązano nierówność cosu >		w
	3		2

przedziale

	π		π
[0,		) , które wynosi u ∊ [0,		) i wrócono do zniennej wyjściowej.
	2		3

	π		π		π
Jeśli u =		, to x =		: 3 =
	x		3		9

Jerzy:

	π
W ostaniej linijce miało byc: Jeśli u =		, to ........ oczywiscie
	3

anonim123:

	pi		pi		5
A dlaczego		jak na moim wykresie jedna druga jest przyjmowana dla		i
	3		6		6pi

?

Jerzy: Jakie jest rozwiązanie nierówności cosu > 1/2 w przedziale [0,π/2) ?

anonim123: Właśnie tego nie jestem w stanie wyliczyć prawidłowo.

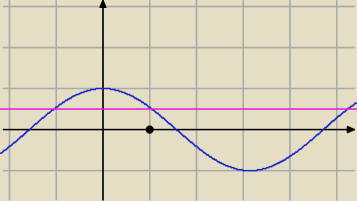
Jerzy: Kropka, to π/3 Fioletowa linia to prosta: y = 1/2 Wyres cosx w przedziale [0,90) leży nad prostą w przedziale [0,π/3)

anonim123: Aha ja narysowałam funkcję sinus zamiast cosinusa

anonim123: Dziękuję za pomoc.