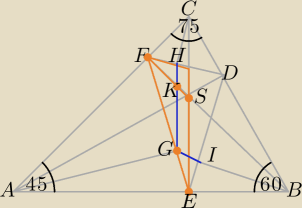
 Ortocentrum trójkąta ABC (punkt S) jest środkiem okręgu wpisanego w trójkąt DEF i jest
punktem przecięcia dwusiecznych kątów wewnętrznych trójkąta DEF.
|∡FES| = |∡SED| = x, |∡BSD| = |∡SDF| = y, |∡DFS| = |∡EFS| = z
Na czworokątach: EBDS, DCFS, AESF można opisać okrąg, stąd |∡DSE| = 120o,
|∡DSF| = 105o, |∡FSE| = 135o,
Po rozwiązaniu układu równań:
ΔDSE: x + y + 120o = 180o
ΔDSF: y + z + 105o = 180o,
ΔFSE: x + z + 135o = 180o
otrzymujemy: x = 15o, y = 45o, z = 30o., trójkąt EDF jest prostokątny.
Niech |EB| = c ⇒ |EC| = |AE| = c√3
W prostokątnych trójkątach:
ΔAEG: |∡AEG| = 90o − x = 75o
ΔBEI: |∡BEI| = 90o − x = 75o, zatem te trójkąty są podobne w skali k = √3,
stąd |EI| = b ⇒ |EG| = c√3.
Korzystając z twierdzenia cosinusów w trójkącie GEI, w którym |∡GEI| = 2x = 30o,
otrzymujemy |GI| = b, więc trójkąt GEI jest równoramienny i |∡EGI| = 30o.
Proszę kontynuować dalej samodzielnie.
W tej figurze jest wiele ciekawych zależności.
Ortocentrum trójkąta ABC (punkt S) jest środkiem okręgu wpisanego w trójkąt DEF i jest
punktem przecięcia dwusiecznych kątów wewnętrznych trójkąta DEF.
|∡FES| = |∡SED| = x, |∡BSD| = |∡SDF| = y, |∡DFS| = |∡EFS| = z
Na czworokątach: EBDS, DCFS, AESF można opisać okrąg, stąd |∡DSE| = 120o,
|∡DSF| = 105o, |∡FSE| = 135o,
Po rozwiązaniu układu równań:
ΔDSE: x + y + 120o = 180o
ΔDSF: y + z + 105o = 180o,
ΔFSE: x + z + 135o = 180o
otrzymujemy: x = 15o, y = 45o, z = 30o., trójkąt EDF jest prostokątny.
Niech |EB| = c ⇒ |EC| = |AE| = c√3
W prostokątnych trójkątach:
ΔAEG: |∡AEG| = 90o − x = 75o
ΔBEI: |∡BEI| = 90o − x = 75o, zatem te trójkąty są podobne w skali k = √3,
stąd |EI| = b ⇒ |EG| = c√3.
Korzystając z twierdzenia cosinusów w trójkącie GEI, w którym |∡GEI| = 2x = 30o,
otrzymujemy |GI| = b, więc trójkąt GEI jest równoramienny i |∡EGI| = 30o.
Proszę kontynuować dalej samodzielnie.
W tej figurze jest wiele ciekawych zależności.

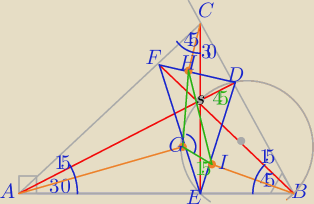 Kąty w trójkącie spodkowym EDF.
1) Miary kątów w odpowiednich trójkątach prostokątnych zapisane niebieskim kolorem.
2) Miary kątów wpisanych okrąg opisany na EBDS zapisane zielonym kolorem
3) S jest punktem przecięcia dwusiecznych kątów wewnętrznych ΔEDF
stąd
|∡E|=30o, |∡D|=90o, |∡F|=60o
4)
I na razie widzę dalej tak jak u Ciebie. Chcę dalej uniknąć rachunków.
Dobranoc). Dalej będzie jutro.
Kąty w trójkącie spodkowym EDF.
1) Miary kątów w odpowiednich trójkątach prostokątnych zapisane niebieskim kolorem.
2) Miary kątów wpisanych okrąg opisany na EBDS zapisane zielonym kolorem
3) S jest punktem przecięcia dwusiecznych kątów wewnętrznych ΔEDF
stąd
|∡E|=30o, |∡D|=90o, |∡F|=60o
4)
I na razie widzę dalej tak jak u Ciebie. Chcę dalej uniknąć rachunków.
Dobranoc). Dalej będzie jutro.


| √6 − √2 | ||
No to jedziemy dalej. Przyda się przy rozwiązywaniu: sin15o = | ||
| 4 |
