planimetria
anonim123: Dany jest trapez ABCD oraz dwa styczne okręgi o środkach w punktach B i C. Uzasadnij że kąt DEA
jest kątem prostym.
Doszłam do tego że miara kąta BEA+miara kąta DEA+miara kąta DEC=180 stopni. Co należy zrobić
dalej?
9 kwi 18:28
a7: a możesz powiedzieć, gdzie jest punkt E?
9 kwi 18:31
a7: albo zrobić rysunek?
9 kwi 18:31
anonim123:
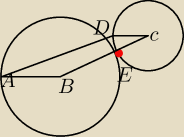
E jest punktem styczności okręgów
9 kwi 18:35
a7:
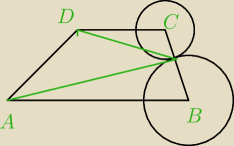
ale jaka jest treść zadania bo na moim rysunku nijak nie wychodzi 90 stopni
9 kwi 18:38
a7:
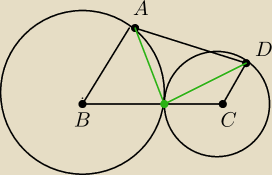
9 kwi 18:43
a7: ?
9 kwi 18:44
anonim123: Treść zadania podałam prawidłowo.
9 kwi 18:54
Mila:
Rysunek był dany?
9 kwi 18:55
a7:
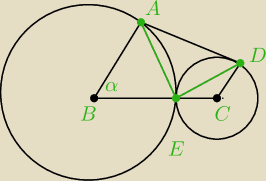
∡ABC=α ∡BCD=180−α
| | 180−α | | 180−(180−α) | | α | |
∡AEB= |
| (trókąt ABE jest równoramienny) ∡DEC= |
| = |
| (trójkąt DEC |
| | 2 | | 2 | | 2 | |
jest równoramienny)
| | 180−α | | α | | α | | α | |
∡AED=180−∡AEB−∡DEC=180− |
| − |
| =180−90+ |
| − |
| = 90 c.n.w |
| | 2 | | 2 | | 2 | | 2 | |
9 kwi 19:01
9 kwi 19:09
a7: 19:01 to dobre rozwiązanie
9 kwi 19:12
Mila:
No to już masz rozwiązanie.
9 kwi 19:17
9 kwi 19:32
a7: tak
9 kwi 19:41
anonim123: A jak, bo nie mogę do tego dojść

9 kwi 19:41
a7: ∡ABE+∡BCD=180
180=180−2α+180−2β czyli α+β=90 czyli szukany ∡AED=180−α−β=180−(α+β)=180−90=90
9 kwi 19:43
a7: (∡ABE+∡BCD=180o gdyż w trapezie zawsze suma kątów przy dowolnym ramieniu jest równa 180o)
9 kwi 19:44
anonim123: Dziękuję

9 kwi 19:44
a7: no, ale rozumiesz?, czy tylko przepiszesz?

9 kwi 19:46
anonim123: robiłam tak samo tylko zapomniałam podzielic przez 2 180 w pierwszym równaniu i wychodziło że
alfa + beta =180
9 kwi 19:51
a7: ok

9 kwi 20:08
rafu: Rozwiąż równania:
a) 1/(2−x)−1=(6−x)/(3x2−12)
b) 12/|x−4| =x
pomóżcie jak najszybciej plz
9 kwi 20:52
 E jest punktem styczności okręgów
E jest punktem styczności okręgów
 ale jaka jest treść zadania bo na moim rysunku nijak nie wychodzi 90 stopni
ale jaka jest treść zadania bo na moim rysunku nijak nie wychodzi 90 stopni

 ∡ABC=α ∡BCD=180−α
∡ABC=α ∡BCD=180−α



