Rownoleglobok Tosia: Na boku LM rownolegloboku KLMN wybrano punkt P. Prosta KP przecina przekątna NL w punkcie Q, a prosta NM w punkcie R. Wykaz że |KQ| = √|QP| * |QR|

Leszek: Cos nie tak jest z trescia zadania , sprawdz ! Prosta NM to bok rownolegloboku !

wredulus_pospolitus: chodzi o przedłużenie boku NM

Leszek: To by sie zgadzalo .

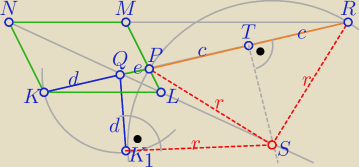
Bogdan: |KQ| = |K₁Q| = d, |QP| = e, |PT| = |TR| = c, Teza: d = √ e*(e + 2c) Dowód: Tworzymy konstrukcję: . 1) z punktu Q kreślimy łuk o promieniu d 2) z punktu T (środek PR) prowadzimy prostopadłą do PR (symetralna PR) 3) rysujemy prostą przez punkty N, Q, L do przecięcia z symetralną PR i zaznaczamy wspólny punkt tych prostych, to punkt S 4) z punktu S zataczamy łuk o promieniu długości |SR| = |SP| = r do przecięcia z łukiem z punktu 1), te łuki przecinają się w punkcie K₁, odcinek QK₁ jest styczny do okręgu o środku S i promieniu r Stosując twierdzenie o siecznej okręgu otrzymujemy: d² = e*(e + 2c) ⇒ d = √ e*(e + 2c) co kończy dowód