 więc tak:
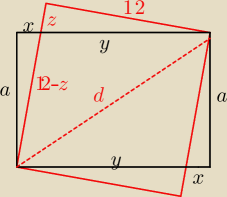
d = 12√2
a2 + (y+x)2 = d2
a2 + x2 = (12−z)2
122 + z2 = y2
36 = 144 − z*12
Pprostokąta = 36 + a*x
Masz układ czterech równań z czterema niewiadomymi ... wyznacz 'a' i 'x'. Podstaw do wzoru na
pole prostokąta, które Ci napisałem
więc tak:
d = 12√2
a2 + (y+x)2 = d2
a2 + x2 = (12−z)2
122 + z2 = y2
36 = 144 − z*12
Pprostokąta = 36 + a*x
Masz układ czterech równań z czterema niewiadomymi ... wyznacz 'a' i 'x'. Podstaw do wzoru na
pole prostokąta, które Ci napisałem
 Wredulus "kocha" układy równań z kilkoma niewiadomymi
Wredulus "kocha" układy równań z kilkoma niewiadomymi  Można tak:
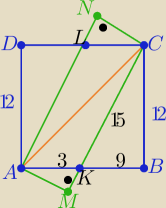
Oznaczenia na rys . dodaj komentarze..............
i ΔAMK podobny do ΔBKC w skali k=1/5
P(BKC)= 54 to P(AMK)= 54/25= 2,16
P(AMCN) = 36+2*2,16 = 40,32
=========================
Można tak:
Oznaczenia na rys . dodaj komentarze..............
i ΔAMK podobny do ΔBKC w skali k=1/5
P(BKC)= 54 to P(AMK)= 54/25= 2,16
P(AMCN) = 36+2*2,16 = 40,32
=========================
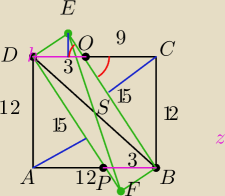 a=12 PKwadratu=144 d=12√2
144−36=108 108:2=54
PΔOCB=54 OC=AP=9 OD=PB=3
z tw. Pitagorasa
OB=DP=15
z podobieństwa ΔDOE i ΔOCB (k, k,k)
hDAP=7,2
15/7,2=3/hDOE hDOE=1,44
PPROSTOKĄTA=36+2*1/2*3*1,44=40,32
a=12 PKwadratu=144 d=12√2
144−36=108 108:2=54
PΔOCB=54 OC=AP=9 OD=PB=3
z tw. Pitagorasa
OB=DP=15
z podobieństwa ΔDOE i ΔOCB (k, k,k)
hDAP=7,2
15/7,2=3/hDOE hDOE=1,44
PPROSTOKĄTA=36+2*1/2*3*1,44=40,32

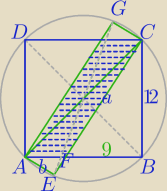 Bez podobieństwa:
1) |AC|=12√2
Bez podobieństwa:
1) |AC|=12√2
| 1 | ||
[FBC]=(144−36):2=54⇔ | *|BF|*12=54 | |
| 2 |