Równanie okręgu wpisanego w romb
Shizzer:
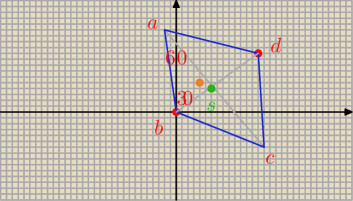
Punkty B = (0, 0) i D = (4, 2) są wierzchołkami kątów rozwartych rombu ABCD. Napisz równanie
okręgu wpisanego w ten romb wiedząc, że kąt ostry rombu ma miarę 60
o
Poprawna odpowiedź: (x−2)
2 + (y − 1)
2 =
√15{4}
Długo rozwiązuję to zadanie chociaż wydaje mi się naprawdę łatwe. Być może robię gdzieś błąd
myślowy albo rachunkowy. W każdym razie chciałbym tylko wiedzieć, w którym momencie popełniam
błąd, że nie wychodzi mi poprawna odpowiedź.
W rombie przekątne dzielą się na połowy, są do siebie prostopadłe i zawierają się w
dwusiecznych
kąta. Więc środek okręgu wpisanego w romb jest środkiem symetrii tego rombu, czyli punktem
przecięcia przekątnych. Skoro przekątne dzielą sie na połowy to punkt S jest środkiem odcinka
|BD|.
S = (4 / 2, 2 / 2) = (2, 1)
Równanie okręgu wpisanego w romb:
(x − 2)
2 + (y − 1)
2 = r
2
Promień jest wysokością jednego z czterech trójkątów prostokątnych powstałych wewnątrz rombu.
Weźmy na przykład trójkąt SBA.
Długość przyprostokątnej |BS|:
|BS| =
√(−2)2 + (−1)2 =
√5
Z funkcji trygonometrycznych:
tg60
o = |BS| / |AS|
√3 =
√5 / |AS| / * |AS|
√3|AS| =
√5 / :
√3
|AS| =
√5 /
√3 =
√15 / 3
Powstają 2 trójkąty podobne na podst. cechy KKK gdzie promień jest przyprostokątną naprzeciw
kąta 60
o. Znów z funkcji trygonometrycznych:
sin60
o = r / |AS|
√3 / 2 = r / (
√15 / 3)
√45 / 3 = 2r / :2
r =
√45 / 6
r
2 = 45 / 36 = 5 / 4
Za każdym razem ten wynik mi wychodzi podczas obliczania promienia i nie mam pojęcia co robię
źle dlatego chciałbym Was bardzo prosić o pomoc w rozwiązaniu tej zagadki

 Punkty B = (0, 0) i D = (4, 2) są wierzchołkami kątów rozwartych rombu ABCD. Napisz równanie
okręgu wpisanego w ten romb wiedząc, że kąt ostry rombu ma miarę 60o
Poprawna odpowiedź: (x−2)2 + (y − 1)2 = √15{4}
Długo rozwiązuję to zadanie chociaż wydaje mi się naprawdę łatwe. Być może robię gdzieś błąd
myślowy albo rachunkowy. W każdym razie chciałbym tylko wiedzieć, w którym momencie popełniam
błąd, że nie wychodzi mi poprawna odpowiedź.
W rombie przekątne dzielą się na połowy, są do siebie prostopadłe i zawierają się w
dwusiecznych
kąta. Więc środek okręgu wpisanego w romb jest środkiem symetrii tego rombu, czyli punktem
przecięcia przekątnych. Skoro przekątne dzielą sie na połowy to punkt S jest środkiem odcinka
|BD|.
S = (4 / 2, 2 / 2) = (2, 1)
Równanie okręgu wpisanego w romb:
(x − 2)2 + (y − 1)2 = r2
Promień jest wysokością jednego z czterech trójkątów prostokątnych powstałych wewnątrz rombu.
Weźmy na przykład trójkąt SBA.
Długość przyprostokątnej |BS|:
|BS| = √(−2)2 + (−1)2 = √5
Z funkcji trygonometrycznych:
tg60o = |BS| / |AS|
√3 = √5 / |AS| / * |AS|
√3|AS| = √5 / : √3
|AS| = √5 / √3 = √15 / 3
Powstają 2 trójkąty podobne na podst. cechy KKK gdzie promień jest przyprostokątną naprzeciw
kąta 60o. Znów z funkcji trygonometrycznych:
sin60o = r / |AS|
√3 / 2 = r / (√15 / 3)
√45 / 3 = 2r / :2
r = √45 / 6
r2 = 45 / 36 = 5 / 4
Za każdym razem ten wynik mi wychodzi podczas obliczania promienia i nie mam pojęcia co robię
źle dlatego chciałbym Was bardzo prosić o pomoc w rozwiązaniu tej zagadki
Punkty B = (0, 0) i D = (4, 2) są wierzchołkami kątów rozwartych rombu ABCD. Napisz równanie
okręgu wpisanego w ten romb wiedząc, że kąt ostry rombu ma miarę 60o
Poprawna odpowiedź: (x−2)2 + (y − 1)2 = √15{4}
Długo rozwiązuję to zadanie chociaż wydaje mi się naprawdę łatwe. Być może robię gdzieś błąd
myślowy albo rachunkowy. W każdym razie chciałbym tylko wiedzieć, w którym momencie popełniam
błąd, że nie wychodzi mi poprawna odpowiedź.
W rombie przekątne dzielą się na połowy, są do siebie prostopadłe i zawierają się w
dwusiecznych
kąta. Więc środek okręgu wpisanego w romb jest środkiem symetrii tego rombu, czyli punktem
przecięcia przekątnych. Skoro przekątne dzielą sie na połowy to punkt S jest środkiem odcinka
|BD|.
S = (4 / 2, 2 / 2) = (2, 1)
Równanie okręgu wpisanego w romb:
(x − 2)2 + (y − 1)2 = r2
Promień jest wysokością jednego z czterech trójkątów prostokątnych powstałych wewnątrz rombu.
Weźmy na przykład trójkąt SBA.
Długość przyprostokątnej |BS|:
|BS| = √(−2)2 + (−1)2 = √5
Z funkcji trygonometrycznych:
tg60o = |BS| / |AS|
√3 = √5 / |AS| / * |AS|
√3|AS| = √5 / : √3
|AS| = √5 / √3 = √15 / 3
Powstają 2 trójkąty podobne na podst. cechy KKK gdzie promień jest przyprostokątną naprzeciw
kąta 60o. Znów z funkcji trygonometrycznych:
sin60o = r / |AS|
√3 / 2 = r / (√15 / 3)
√45 / 3 = 2r / :2
r = √45 / 6
r2 = 45 / 36 = 5 / 4
Za każdym razem ten wynik mi wychodzi podczas obliczania promienia i nie mam pojęcia co robię
źle dlatego chciałbym Was bardzo prosić o pomoc w rozwiązaniu tej zagadki 
 Na odwrót
Na odwrót  ∡BAD = 60o więc ∡ABC = 120o więc:
∡BAS = 30o więc ∡ABS = 60o
∡BAD = 60o więc ∡ABC = 120o więc:
∡BAS = 30o więc ∡ABS = 60o 

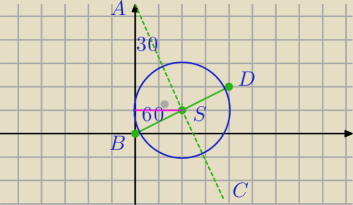 tg60=|AS|/|BS| AS=......
sin30=r/|AS| r=.............
tg60=|AS|/|BS| AS=......
sin30=r/|AS| r=.............
