Dowód, trygonometria i trójkąt Mateusz: Wykaż, że w każdym trójkącie prawdziwa jest równość (b+c)cosα + (c+a)cosβ + (a+b)cosγ = a+b+c Domyślam się, że należy skorzystać z twierdzenia cosinusów, ale za bardzo nie wiem, jak to zacząć. Proszę o pomoc

wredulus_pospolitus: rozumiem, że α to kąt naprzeciwko boku a β jest naprzeciwko b a γ na przeciwko boku c

wredulus_pospolitus: jeżeli nie −−− to dodaj rysunek

Mateusz: Nie ma rysunku do zadania, czyli pewnie tak: α to kąt naprzeciwko boku b itd

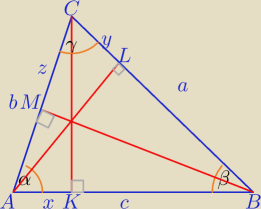
Mila: 1) W ΔAKC i w ΔCKB:

	x
cosα=		⇔x=b*cosα
	b

	c−x
cosβ=		⇔c−x=a*cosβ ⇔c=b*cosα+a* cosβ
	a

2) W ΔALC i w ΔALB:

	y
cosγ=		⇔y=b*cosγ
	b

	a−y
cosβ=		⇔a−y=c*cosβ ⇔a=b*cosγ+c*cosβ
	c

3)W ΔCMB i w ΔAMB:

	z
cosγ=		⇔z=a cosγ
	a

	b−z
cosα=		⇔b−z=c*cosα ⇔b=a cosγ+c*cosα
	c

4) a+b+c=b*cosγ+c*cosβ+a cosγ+c*cosα+b*cosα+a* cosβ ⇔ a+b+c=(b+c) cosα+(a+c) cosβ+(a+b) cosγ ================================== cnw

Mateusz: Dziękuję bardzo !