Własności prawdopodobieństwa Layla: Niech A,B⊂Ώ. Oblicz P(A'uB) i P(A\B), jeśli wiadomo, że P(A)=²₃, P(B')=³₄ oraz P(AuB)=³₄ Odp powinno wyjść: P(A\B)=²₃, P(A'uB)=¹₂ Niech A,B⊂Ώ. Oblicz P(A'\B), jeśli wiadomo, że AuB jest zdarzeniem pewnym oraz P(A)=P(B)=3P(AnB) Odp powinno wyjść: P(A'\B)=²₃ Dane są zdarzenia A,B⊂Ώ takie, że P(B)≥0. Wykaż, że: P(A\B)≥^{P(A)+P(B)−1}_P(B)

Layla:

	2		3		3
P(A)=		P(B')=		P(AuB)=
	3		4		4

wredulus_pospolitus: 3) Trudno udowodnić coś co NIE JEST prawdą. Tam powinno być P(A|B)

wredulus_pospolitus: sprawdź w poprzednich podpunktach czy masz na pewno P(A\B) czy może jednak P(A|B)

ite: zad. 1 wykorzystaj wzór P(A\B) = P(A∪B) − P(B)

wredulus_pospolitus: i uzupełnienie do zad 1: oraz ze wzoru P(A' u B) = 1 − P(A\B)

Layla: Masz rację, ma być P(A|B)

wredulus_pospolitus: zad 2.

	3		1
Więc wiemy, że P(AuB) = 1 ; P(A) = P(B) =		; P(AnB) =
	5		5

P(A'\B) = P(A'nB') = 1 − P(AuB) więc raczej nie chodziło tutaj o P(A' \ B)

ite: Rzeczywiście przy tych danych, jeśli jest różnica (A\B), to wyniki się nie zgadzają. Ale to już zmartwienie autora.

Layla: Chyba tak, bo ja sobie popatrzyłam na to jak na P(A'\B) i liczyłam to i mi właśnie wynik nie wychodził P(A\B)= P(A)−P(B) ?

wredulus_pospolitus: Zacznijmy od tego ... pisząc znak \ myślisz o znaku \ czy o znaku | Bo P(A\B) i P(A|B) to CAŁKOWICIE inne prawdopodobieństwa Dodatkowo: P(A\B) = P(A) − P(B) to jest BZDUUUURA

Layla: To w takim razie jak wygląda P(A\B) mówimy o \ znaku

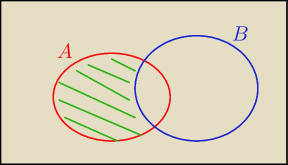
wredulus_pospolitus: P(A\B) = P(zielonego obszaru) = P(A) − P(A n B) P(A\B) = P(zielonego obszaru) = P(A u B) − P(B) Przykładowe sposoby zapisania

Layla: To w sumie, ma sens. Dziękuje Teraz spróbuję to sobie przeliczyć. A jeszcze jedno pytanie jak mam w zapisie znak | to co to znaczy. Jaką część zbiorów mam wziąć?

wredulus_pospolitus: | uzwamy w przypadku prawdopodobieństwa warunkowego

	P(A n B)
P(A | B) =
	P(B)

Layla: Ok, a zadanie 3 przy zapisie P(A|B) potrafisz udowodnić?

wredulus_pospolitus:

	P(AnB)
L =
	P(B)

	P(A) + P(B) − 1		P(AuB) + P(AnB) − 1		1 + P(AnB) − 1
P =		=		≤		=
	P(B)		P(B)		P(B)

	P(AnB)
=		= L
	P(B)

Zastosowany został wzór: P(AuB) = P(A) + P(B) − P(AnB) a raczej tenże wzór ale w postaci: P(AuB) + P(AnB) = P(A) + P(B)

wredulus_pospolitus: A także skorzystaliśmy z 'oczywistej oczywistości' czyli, że P(AuB) ≤ 1

wredulus_pospolitus: Matura rozszerzona czy podstawowa

Layla: Rozszerzona ale prawdopodobieństwo dla mnie to czarna magia. Nie ma gorszego działu

wredulus_pospolitus: Wielu osobom prawdopodobieństwo stwarza problemy, ale nie dlatego że jest to 'trudniejszy' dział, co wymaga od ucznia niestety myślenia kombinatorycznego. Zasmucę Cię jeszcze tym − że te zadania tutaj były de facto opierały się o logikę i zbiory. Jeżeli poważnie podchodzisz do matury i chcesz się nauczyć rozwiązywać zadania z prawdopodobieństwa, to mogę Ci podać kontakt na discordzie gdzie każdego dnia siedzimy (wraz z paroma maturzystami) i przerabiamy zadania.

Layla: W sumie poproszę o ten kontakt.

wredulus_pospolitus: Brzydalos#5694