Rozwiąże ktoś? PjoterOOO: Podstawą graniastosłupa prostego jest równoległobok o bokach a i b i kącie ostrym α. Krótsza przekątna graniastosłupa ma długość d. Oblicz pole powierzchni całkowitej tego graniastosłupa.

PjoterOOO:

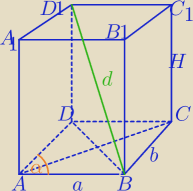
Mila: a>b 1) P_ABCD=a*b*sinα 2) W ΔBAD: |DB|²=a²+b²−2abcosα 3) W ΔD₁DB: d²=|DB|²+H² H=√d²−a²−b²+2ab cosα P_c=2*a*b*sinα+(2a+2b)*H P_c=....

mann: A czemu dolna podstawa jest bardziej widoczna niż górna Mila? Kłopoty z rysunkami?

Mila: To popraw

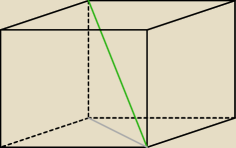
mann: Proszę bardzo. Podstawy tego graniastosłupa leżą przecież w równoległych płaszczyznach, czy to rozumiesz? A na Twoim rysunku te płaszczyzny nie są równolegle i bez obrazy. Bolączką wielu, bardzo wielu nauczycieli uczących matematykę jest nieumiejętność sporządzania poprawnie rysunków.

a7: sorry mann , ale z tych dwóch rysunków wybieram Mili 100% przypatrz się i zobacz, który jest bardziej metodyczny i który lepiej pokazuje to, co trzeba zobaczyć

mann: Następny, który nie widzi, że dolna podstawa i górna nie leżą w równoległych płaszczyznach na rysunku Mili

WhiskeyTaster: A na Twoim rysunku niewiele zaznaczysz. Stąd wyższość rysunku Mili nad Twoim. Czemu nie zaznaczyłeś drugiej przekątnej podstawy i kąta przy krawędziach? Rysunek jest tylko poglądowy.

PjoterOOO: Czy potem wystarczy za H podstawić wyrażenie pod pierwiastkiem i całe wyrażenie zostawić? Czy trzeba redukować, o ile się da w tym przypadku?

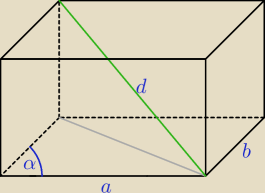
mann: można? można