trapez
Patryk : Dany jest trapez ABCD w którym podstawy mają długość AB=10 i CD=6. Przez punkt E (środek boku
AD) poprowadzono prosta równoległa do podstaw trapezu. Przecięła ona bok BC, przekątna AC oraz
przekątna BD w punktach odpowiednio F,G,H. Przekątne trapezu przecinają się w punkcie P.
Oblicz stosunek pola trójkata GHP do pola trójkata ABP
7 kwi 18:56
Patryk : Umie ktoś pomoc?
7 kwi 19:30
7 kwi 20:25
Eta:
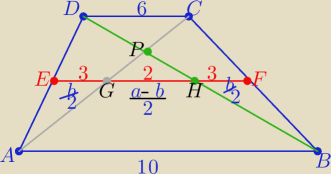
7 kwi 20:38
Saizou :
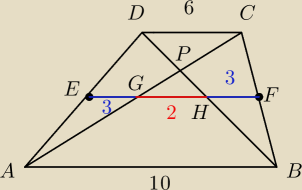
ΔABP ~ ΔGHP (kkk)
7 kwi 20:38
Eta:
Wrrrrrrrrrrrrrrrrrrrrrrrrr

7 kwi 20:38
7 kwi 20:41
Patryk : Moglibyście wytłumaczyć skąd wzięły się te odcinki 3,2,3?
7 kwi 22:18
wredulus_pospolitus:
z podobieństw trójkątów
np. ΔAEG i ΔADC mamy 'lewą 3' ... analogicznie prawą
'2' to konsekwencja powyższego
7 kwi 22:33
Saizou :
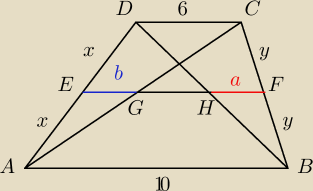
ΔACD ~ ΔAGE (kkk)
analogicznie z trójkątami ΔBFH oraz ΔBCD, zatem a = 3
| | 6+10 | |
EF łączy środki ramion trapezu i ma długość |
| =8 (pokaż to sam) |
| | 2 | |
GH = 8 − 6 = 2
7 kwi 22:37
Eta:
Czytaj co napisałam na rysunku :
7 kwi 22:37
wredulus_pospolitus:
Etuś −−− ale tak dowiedział się w jaki sposób powstało to co napisałaś na rysunku

7 kwi 22:53
Eta:
A tak się dowie ( i zapamięta)że zawsze tak jest w dowolnym trapezie !

7 kwi 22:56
wredulus_pospolitus:
Etuś −−− wierzysz w to, ze zapamięta

Jak nie będzie rozumiał skąd 'to wyszło'

7 kwi 22:58
Patryk: Saizou dzięki

7 kwi 23:10
Eta:

7 kwi 23:10

 ΔABP ~ ΔGHP (kkk)
ΔABP ~ ΔGHP (kkk)

 ΔACD ~ ΔAGE (kkk)
ΔACD ~ ΔAGE (kkk)


 Jak nie będzie rozumiał skąd 'to wyszło'
Jak nie będzie rozumiał skąd 'to wyszło' 

