Prostokąt Fox12: Długości boków AB i BC prostokąta ABCD są równe odpowiednio 10 i 9. Na przekątnej BD leży punkt E, przy czym |BE| : |ED| = 1 : 3. Prosta AE przecina bok BC w punkcie F, a przedłużenie boku DC w punkcie G. Oblicz długości odcinków BF i CG

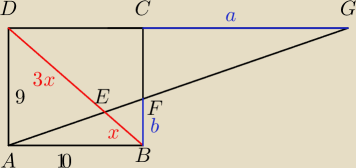
Saizou : ΔABE ~ ΔGDE (kkk)

x		3x
	=
10		a+10

x z Pitagorasa

Fox12: Dzięki

Fox12: A ile powinien wyjść x? bo wychodzi trochę dziwny

wredulus_pospolitus: 4x = √10² + 9² <−−− z tw. Pitagorasa

wredulus_pospolitus: ale to nie ma żadnego związku z zadaniem

wredulus_pospolitus: 'x' w proporcji się skraca nam

ICSP: a po co w ogóle liczymy ten x? Przecież i tak się skróci.

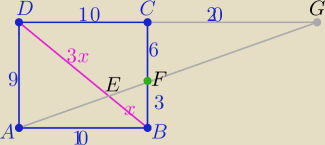
Eta: Z podobieństwa trójkątów ADE i BEF w skali k=3

	1
to |BF|=		|AD|= 3 więc |CF|=6
	3

======== i z podobieństwa trójkątów DEG i ABE w skali k=3 to |DG|=3*10 =30 ⇒ |CG|=20 =========

Eta: |BF|=3 =======

Fox12: Dzięki

szkoła: Możecie zerknąć na to https://matematykaszkolna.pl/forum/399569.html