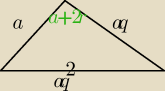
katy trojkat boki zadanko: Oblicz miary kątów trójkąta w którym dlugosci bokow tworza ciag geometryczny a miary katow ciag arytm. a²q⁴=a²+a²q²−2a²qcos(a+2r) ...

	q2+1−q4
cos(a+2r)=
	q2

q⁴−q²−1=0 t=q²,t≥0 t²−t−1=0

	1−√5
t1=		(odpada)
	2

	1+√5
t2=
	2

	1+√5
q=√
	2

no i wstawiam dalej Czy sie tu gdzies nie rypnalem?Trzeba rozpatrzyc,czy ciag jest malejacy/rosnacy?A moze calkowicie zly pomysl na zadanie?

PW: Z czego wynika równość cos(a+2r) = 0 − założyłeś, że trójkąt jest prostokątby?

Jerzy: Wskazówka: oznacz katy: α − r , α , α + r i przeciwległe boki: a , aq , aq²

Jerzy: α = 60^o i teraz zapisz tierdzemie cosinusów dla kąta 60^o i oblicz q Okaże się, że trójkąt jest równoboczny.

ICSP: twierdzenie sinusów w tym wypadku będzie wygodniejsze( ze względu na boki tworzące ciąg geometryczny)

zadanko: Wlasnie nie wiem dlaczego ta rownosc zastosowalem,nie mialem pomyslu i przyrownalem prawa strone cos(a+2r) = ... do zera. Rozumiem,dziekuje.A co jezeli np. ciag geometryczny jest rosnacy a ciag arytm malejacy i na odwrot?Nie zmienia to ze tak powiem odpowiadania katow wzgledem bokow?

Jerzy: W każdym trójkącie najkrótszy bok leży naprzeciwko najmniejszego kąta.

zadanko: Wtedy przy malejacym ciagu geom i rosnacym arytm najdluzszy bedzie bok a zamiast aq² naprzeciwko kąta a+2r,myslalem,ze to cos zmienia,dziekuje.

Jerzy: W każdym innym trójkącie jest to niemożliwe.