 Cześć,
mam takie zadanie:
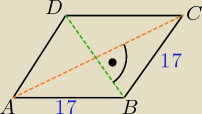
Oblicz pole rombu o boku 17cm, w ktorym dlugości przekatnych roznią się o 14 cm.
zrobiłem tak:
x1 =− przekatna zaznaczona kolorem zielonym
x2 − ( x+ 14) − przekatna zaznaczona kolorem pomaranczowym
Cześć,
mam takie zadanie:
Oblicz pole rombu o boku 17cm, w ktorym dlugości przekatnych roznią się o 14 cm.
zrobiłem tak:
x1 =− przekatna zaznaczona kolorem zielonym
x2 − ( x+ 14) − przekatna zaznaczona kolorem pomaranczowym
| 1 | 1 | |||
( | )2 + ( | (x+14))2 = 172 | ||
| 2 | 2 |
| 1 | 1 | ||
x2 + ( | x + 7)2 = 289 | ||
| 4 | 2 |
| 1 | |
x2 + 14x2 + 7x + 49 = 289 | |
| 4 |
| 1 | |
x2 + 7x − 240 = 0 | |
| 2 |
| 1 | ||
P = | * 29 * 15 = 217,5 cm2 | |
| 2 |
 "skopałeś" rachunki
"skopałeś" rachunki  sprawdź jeszcze raz
sprawdź jeszcze raz
| −7+23 | ||
x1= | = 16
| |
| 1 |
 Podpowiem:
Aby uniknąć błędów wystarczyło wprowadzić oznaczenia
2f −−− długość dłuższej przekątnej , f >0
2e −−− " " krótszej przekątnej , e >0
2f −2e= 14 => f−e= 7 => f = 7+e
f2+e2= 289
policz teraz , masz układ równań , bez ułamków
Podpowiem:
Aby uniknąć błędów wystarczyło wprowadzić oznaczenia
2f −−− długość dłuższej przekątnej , f >0
2e −−− " " krótszej przekątnej , e >0
2f −2e= 14 => f−e= 7 => f = 7+e
f2+e2= 289
policz teraz , masz układ równań , bez ułamków


 ,,, a zapytam, czy Klara to Eta, czy Eta to Klara ?
,,, a zapytam, czy Klara to Eta, czy Eta to Klara ?  Dziekuje za odpowiedz
Dziekuje za odpowiedz 
 Ja nie kwestionuję Twoich oznaczeń, ale unikniesz błędów stosując te ozn. , które
zasugerowałam.
a co do 2 pytania? to."trafione" ! .....pozdrawiam .. η
Ja nie kwestionuję Twoich oznaczeń, ale unikniesz błędów stosując te ozn. , które
zasugerowałam.
a co do 2 pytania? to."trafione" ! .....pozdrawiam .. η 


 bo x2−x1= 14
x1= 16 to x2 = 16+14 = 30
bo x2−x1= 14
x1= 16 to x2 = 16+14 = 30
 ok. jeszcze raz przeanalizuje
ok. jeszcze raz przeanalizuje  mam jeszcze takie zadanie:
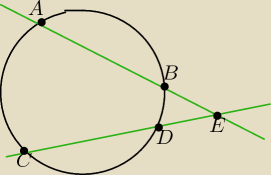
W okregu poprowadzono dwie cieciwy AB i CD, które przecieły sie w punkcie E. Wiedząc, że
|AE| = 9cm; |EB| = 4cm; |CE| = 3 cm, oblicz |ED|.
Nie wiem czy rysunek dobry wykonałem....
Znam tylko jedną własnośc na cięciwe i okrag, ale jest ona uzytecznia w momencie kiedy jedna
cieciwa jest styczna do okregu, wtedy |AB| * |BE| = |CE|2
prosze o pomoc
mam jeszcze takie zadanie:
W okregu poprowadzono dwie cieciwy AB i CD, które przecieły sie w punkcie E. Wiedząc, że
|AE| = 9cm; |EB| = 4cm; |CE| = 3 cm, oblicz |ED|.
Nie wiem czy rysunek dobry wykonałem....
Znam tylko jedną własnośc na cięciwe i okrag, ale jest ona uzytecznia w momencie kiedy jedna
cieciwa jest styczna do okregu, wtedy |AB| * |BE| = |CE|2
prosze o pomoc
 Mam jeszcze takie:
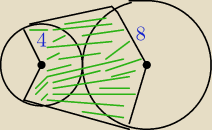
Oblicz pole zacieniowanej figury:
Mam jeszcze takie:
Oblicz pole zacieniowanej figury:
| α | ||
Czy mam skorzystac z tego wzoru: l = 2πr2 * | ? | |
| 360o |
 x
ok
x
ok już jestem byłam
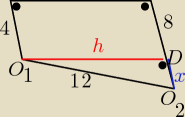
już jestem byłam  zad. 1) skorzystaj z podobieństwa trójkątów; ΔADE ~ ΔCBE
i wyznacz IDEI
zad. 2) widzisz dwa przystające trapezy prostokątne ? (bo ja widzę
zad. 1) skorzystaj z podobieństwa trójkątów; ΔADE ~ ΔCBE
i wyznacz IDEI
zad. 2) widzisz dwa przystające trapezy prostokątne ? (bo ja widzę  podstawami są r1 i r2
ramię trapezu ; Ir1+r2I= 12
podstawami są r1 i r2
ramię trapezu ; Ir1+r2I= 12
| 8−4 | ||
x= | = 2
| |
| 2 |
 i nijak nie wychodzilo x = 2 tylko
rowne 4
dlaczego nalezy jeszcze podzielic ten wynik przez dwa?
i nijak nie wychodzilo x = 2 tylko
rowne 4
dlaczego nalezy jeszcze podzielic ten wynik przez dwa?

 ok, ale tych wczesniejszych
rzeczy nie rozumiem...
ok, ale tych wczesniejszych
rzeczy nie rozumiem...

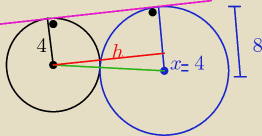 masz rację , teraz widzę,że zamiast x= 4 , pomyłkowo napisałam ( x =2)
sorry
masz rację , teraz widzę,że zamiast x= 4 , pomyłkowo napisałam ( x =2)
sorry  teraz policz to pole
teraz policz to pole
| IAEI | IBEI | |||
= | ||||
| ICEI | IDEI |
| 9 | 4 | |||
= | ||||
| 3 | IDEI |
| 12 | 4 | |||
IDEI= | = | = 113 | ||
| 9 | 3 |
 no dobra, ale nie rozumiem tego jak policzyłaś wysokość. To jest jakas
własność? ze r1 + r2 = 12 ?
no dobra, ale nie rozumiem tego jak policzyłaś wysokość. To jest jakas
własność? ze r1 + r2 = 12 ? 
 dziekuje
dziekuje
| 8+4 | ||
P = | * 4√8 = 24√8cm2 | |
| 2 |
 √8=2√2
√8=2√2 

 !
więc h= 4*2√2= 8√2 ......... bo 64*2= 128
Achhhhh ....... co ja się z Tobą mam
!
więc h= 4*2√2= 8√2 ......... bo 64*2= 128
Achhhhh ....... co ja się z Tobą mam Duże , bbbb duże "czekoladki" mi postawisz
Duże , bbbb duże "czekoladki" mi postawisz
 Przeciez napisals w zadaniu z e p=24 a potem pytasz ile rowna sie pole.
Przeciez napisals w zadaniu z e p=24 a potem pytasz ile rowna sie pole.
| f*e | ||
P= | to jesli f=6 to obliczymy druga przekatna e | |
| 2 |
| 6*e | ||
24= | /*(2) to 48=6*e to e=8 wiec ztgo wynika z edluzsza przekatna ma dlugosc 8 a nie 6 | |
| 2 |